Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Тройные интегралы
Имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.)
I. Вычисление тройных интегралов с помощью повторного интегрирования
1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.
Пусть сначала T = [a, b; c, d; e, f] - прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда
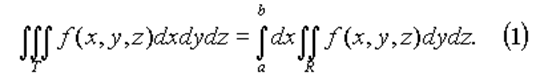
Заменяя в (1) двойной интеграл повторным, получим
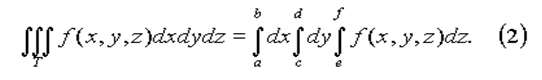
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Если первые два интеграла в (2) объединить в двойной, то будем иметь
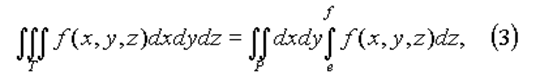
где P = [a, b; c, d] - проекция параллелепипеда T на плоскость xy.
Заметим, что в этих случаях можно менять роли переменных.
2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью x=const, a ≤ x ≤ b представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда
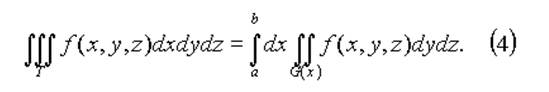
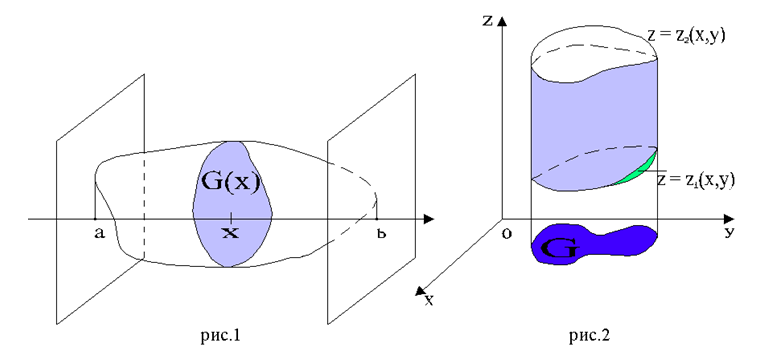
3. Пусть теперь тело T представляет собой "цилиндрический брус", ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z1(x, y) и z2(x, y) - непрерывны в G. Тогда
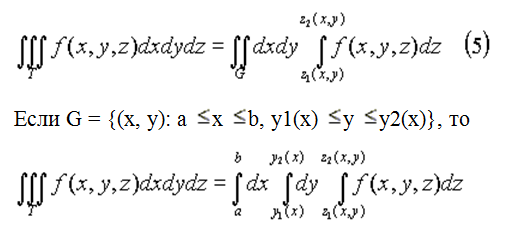
Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.
II. Замена переменных в тройном интеграле  состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
 состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам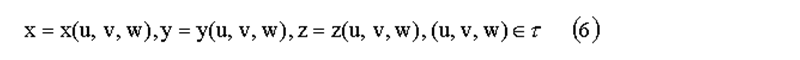
Если выполняются условия

то имеет место формула
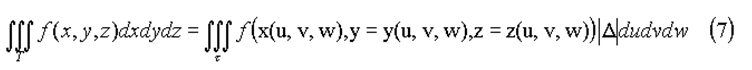
Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.
1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
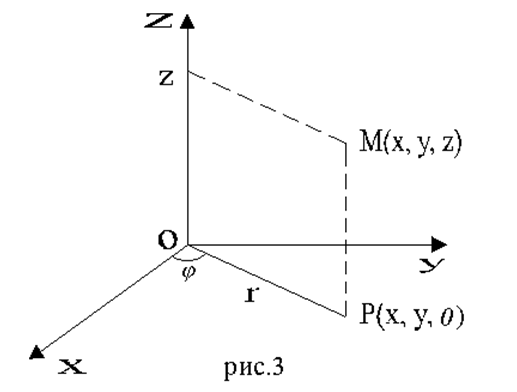
Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел (r,φ,z), где (r,φ) - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
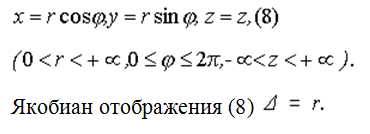
2. Сферические координаты. Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел (r,θ,φ), где r - расстояние точки M до точки 0, θ - угол между лучами OM и OZ, φ - полярный угол точки P на плоскости xy. Тройка чисел (r,θ,φ) называется сферическими координатами точки M.
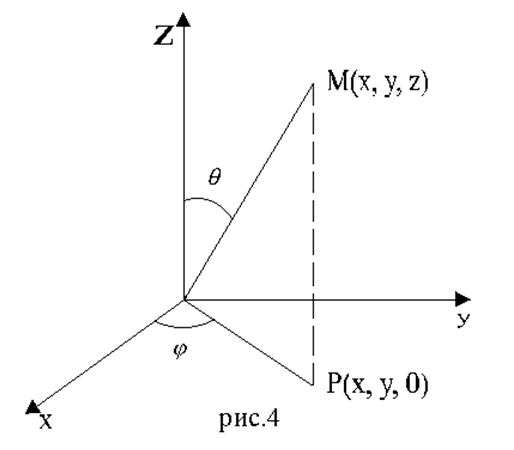
Они связаны с прямоугольными формулами
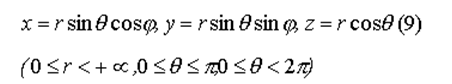
Якобиан отображения

Иногда используются обобщённые сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой

Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
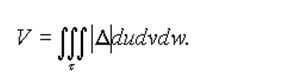
Пусть T - материальное тело (кубируемая область) с плотностью 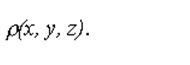
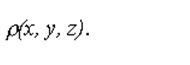
Тогда
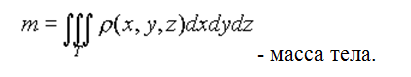
Пример1. Вычислить объём тела, ограниченного поверхностями: x2 + y2 + z2 = a2, x2 + y2 - ax = 0. (рис. 5)
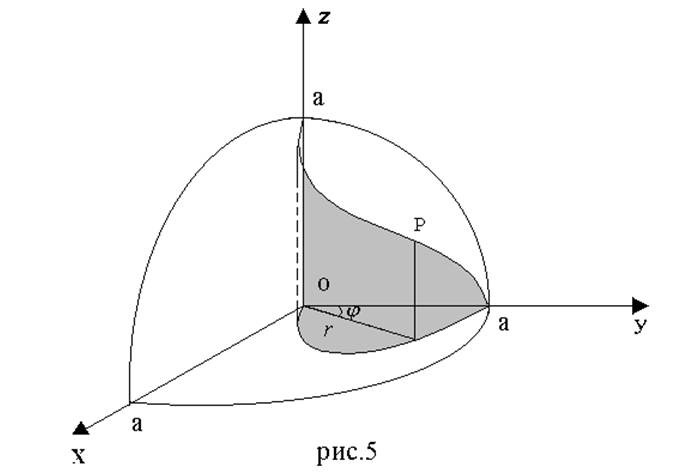
Решение. Рассмотрим одну четвёртую часть тела, лежащую в первом октанте. Часть поверхности \(z={\sqrt {a^2-x^2-y^2}}\) вырезанная цилиндром, проектируется в область
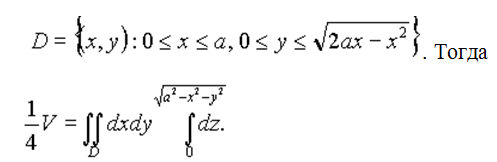
Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? - ax = 0 преобразуется в кривую

Таким образом
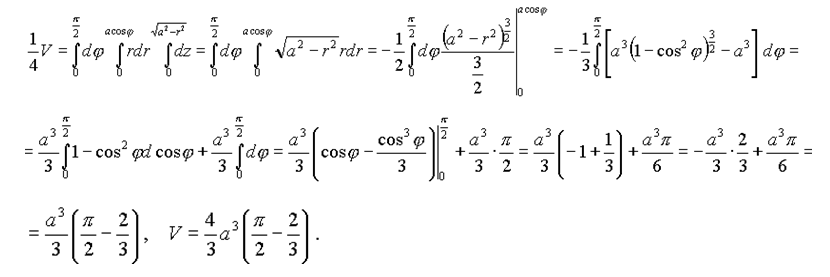
Пример 2. Вычислить интеграл
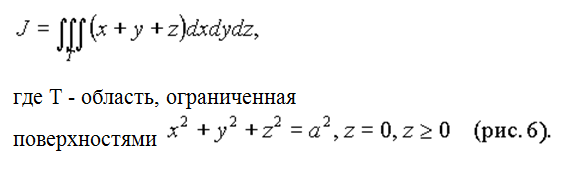
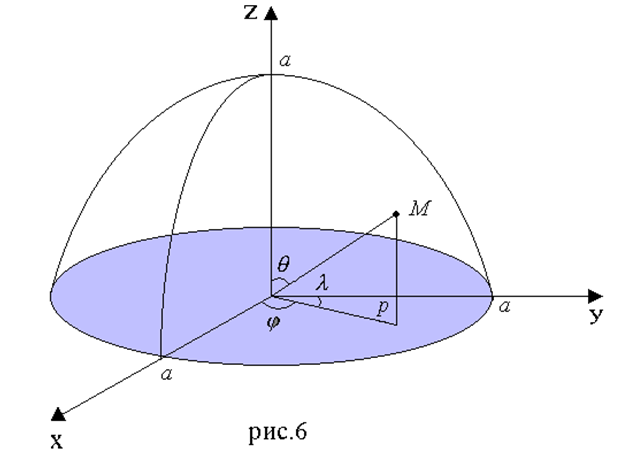
Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами
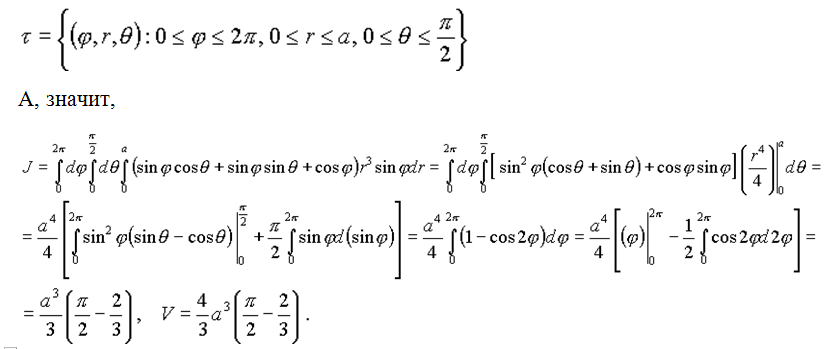
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике -
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор по алгебре
Репетитор по алгебре -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Подготовка к ЕГЭ по английскому онлайн
Подготовка к ЕГЭ по английскому онлайн -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Репетитор по математике впр
Репетитор по математике впр -
 Репетитор для подготовки к ВПР по английскому
Репетитор для подготовки к ВПР по английскому -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

