О платформе 
Премиум математика 
Репетиторы 
Тарифы 
Вход
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 4)
Задача № 1
Найдите корень уравнения:
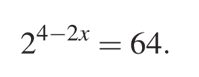
Решение
Перед нами показательное уравнение. Чтобы решить его воспользуемся свойствами степеней.
Сначала сделаем преобразования и получим одинаковые основания в левой и правой части уравнения, в данном случае это будет основание «2».
Известно, что если равны основания степени, то будут равны и выражения, составляющие их степени, это утверждение позволяет нам перейти к более простому уравнению и найти его корень:
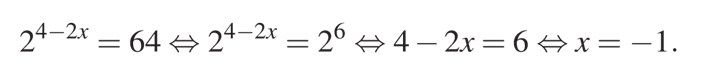
Ответ: −1.
Задача № 2
Найдите корень уравнения:
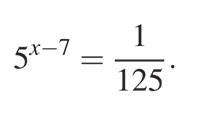
Решение
Перед нами показательное уравнение. Чтобы решить его воспользуемся свойствами степеней.
Сначала сделаем преобразования и получим одинаковые основания в левой и правой части уравнения, в данном случае это будет основание «5».
Известно, что если равны основания степени, то будут равны и выражения, составляющие их степени, это утверждение позволяет нам перейти к более простому уравнению и найти его корень:
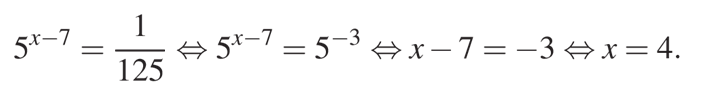
Ответ: 4.
Задача № 3
Найдите корень уравнения:
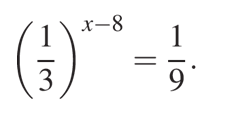
Решение
Перед нами показательное уравнение. Чтобы решить его воспользуемся свойствами степеней.
Сначала сделаем преобразования и получим одинаковые основания в левой и правой части уравнения, в данном случае это будет основание «\(1\over3\)».
Известно, что если равны основания степени, то будут равны и выражения, составляющие их степени, это утверждение позволяет нам перейти к более простому уравнению и найти его корень:
Ответ: 10.
Дарим в подарок бесплатный вводный урок!
Репетиторы
Похожие статьи
Вертикальные углы
Обновлено: 20 авг 2024
Как легко разделить на 0,1; 0,01; 0,001
Обновлено: 01 янв 2025
Как найти делимое?
Обновлено: 01 мар 2025
Куб дроби
Обновлено: 18 ноя 2024
ЕГЭ по математике, профильный уровень. Показательные уравнения
Обновлено: 06 июл 2024
Задачи по финансовой математике
Обновлено: 03 июн 2024
Решаем текстовые задачи
Обновлено: 06 сен 2024
Как перевести минуты в часы
Обновлено: 17 ноя 2024