ЕГЭ по математике, профильный уровень. Задачи по планиметрии

Математика Подготовка к ЕГЭ ЕГЭ по математике

Это задание №16 в ЕГЭ

Условие:

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В - перпендикулярна АМ, и пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а) докажите, что биссектриса угла С делит отрезок МN пополам

б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Решение

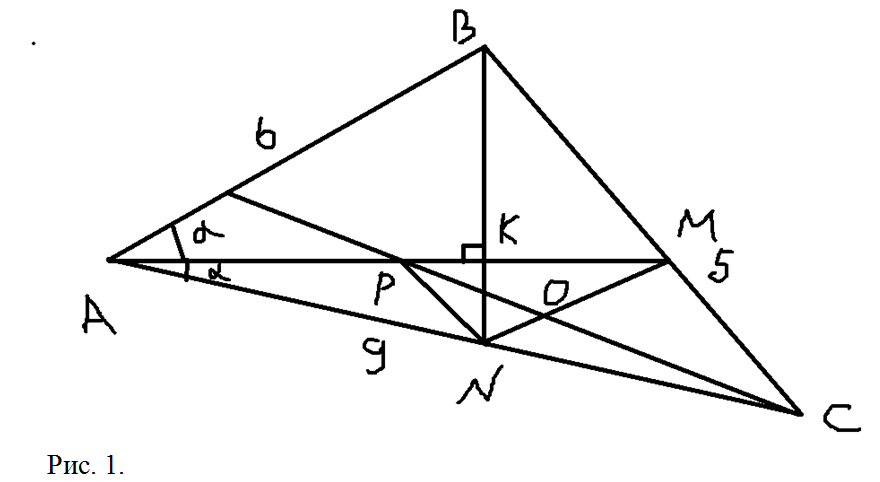
а) В планиметрических задачах важно сделать грамотный и понятный чертеж. Именно чертеж позволяет представить условие задачи графически и увидеть возможное решение визуально. На Рис. 1 изображен треугольник АВС и сделаны дополнительные построения, необходимые для решения этой задачи.

Введем дополнительные обозначения. Обозначим точкой K пересечение отрезков AM и BN. Треугольник ABN будет равнобедренный, так как в нем AK является не только биссектрисой, но и высотой (по условию задачи, угол АВК - прямой). Итак, АВ = АN. По свойству равнобедренных треугольников, AK является и медианой, то есть K — середина BN.

Получаем, что AN = AB = 6, откуда NC = AC − AN = 9 – 6 = 3.

Теперь еще раз рассмотрим треугольник ABC. Известно свойство, по которому биссектриса АМ делит противоположную сторону треугольника на отрезки, пропорциональные прилежащим сторонам:

BM : MC = AB : AC

Зная, что АВ = 6; ВС = 5; АС = 9 , решив пропорцию, получаем:

BM = 2; MC = 3.

Рассмотрим треугольник MNC. В треугольнике MNC мы нашли, что стороны NC и MC равны, следовательно, треугольник MNC — равнобедренный, с основанием MN. Значит, биссектриса угла C также является медианой и высотой. Отсюда получаем, что биссектриса угла С делит отрезок MN пополам. Что и требовалось доказать.

б) Чтобы найти отношение АР : РN, рассмотрим треугольник PMN. Отрезок PO принадлежит прямой CP. Это значит, что он перпендикулярен отрезку MN и делит его пополам. Отсюда следует, что треугольник PMN — равнобедренный с основанием MN. Значит, PM = PN и отношение AP : PN = AP : PM.

В треугольнике AMC CP — биссектриса, поэтому отношение AP : PM = AC : MC = 3 : 1

Ответ: 3 : 1

Автор - Андрей Найденов

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

ЕГЭ по математике, профильный уровень. Задачи по планиметрии

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи