Задачи по финансовой математике

Задание №17 в ЕГЭ
 
Условие:
 
В начале года 5/6 некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е., к концу следующего — 749 у. е. Если первоначально 5/6 суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.
 
Решение
 
В данной задаче у нас два набора условий. Один набор – состоявшийся. Второй – возможный. Возьмем за «х» одну часть имеющейся некоторой суммы денег. Пусть в банк А, у которого исходя из годовой процентной ставки коэффициент повышения вклада равен «у» вложено 5x у.е. денег.  Тогда в банк Б, у которого аналогичный коэффициент равен «t» будет вложено x  у.е. денег.
 
Тогда, в соответствии с условием задачи, мы сможем записать систему и  будем иметь:
 
 
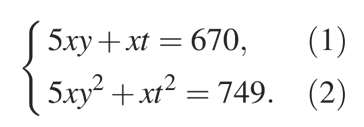
Это «первый набор» условий.
 
Если бы те же суммы были вложены в банки Б и А соответственно, то получится «второй набор» условий. И тогда мы имели бы уравнение:
 
 
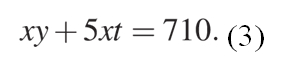
А сумма, которую надо найти, будет равна значению выражения: \(x{y}^2+5x{t}^2\)
 
Рассмотрим и решим систему уравнений (1) и (3).
 
Особенность этой системы в том, что в двух уравнениях у нас имеется три неизвестных. Но для достижения нашей цели, это не помешает:
 
 
 
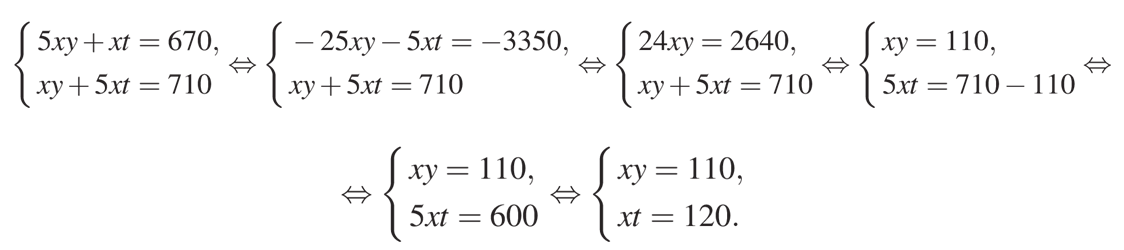
Разделив почленно, получим:
 
 
 
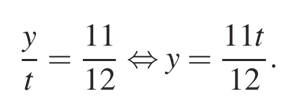
Подставим найденное значение y в уравнение (2) и получим:
 
 
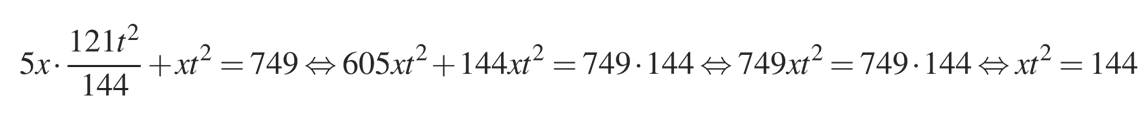
И далее:
 
 
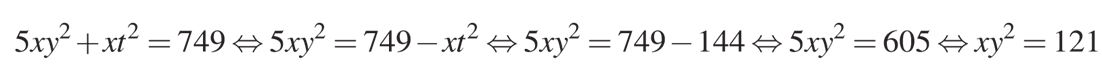
Искомая сумма во втором случае будет найдена из выражения:
 
 
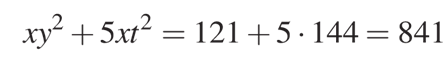
Ответ: 841
 
Автор - Андрей Найденов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Анатольевна Вьюгина
Репетитор по математике
Стаж (лет)
10
Образование:
БГПУ им.М.Танка
Проведенных занятий:
8367
Форма обучения:
Дистанционно (Скайп)
Елена Васильевна Латышевич
Репетитор по математике
Стаж (лет)
17
Образование:
Брестский государственный университет им. А.С. Пушкина
Проведенных занятий:
252
Форма обучения:
Дистанционно (Скайп)
Анастасия Сергеевна Черная
Репетитор по математике
Стаж (лет)
3
Образование:
Кубанский Государственный Университет
Проведенных занятий:
406
Форма обучения:
Дистанционно (Скайп)
Предметы
Специализации
Похожие статьи