Расстояние между точками на координатной прямой

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Расстояние между двумя точками является длиной отрезка, между этими точками. Как найти расстояние между двумя заданными точками?

Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.

Пример . Найдите расстояние между точками:

\(A(-15)\) и \(B(3)\)
\(C(3,2)\) и \(D(7,8)\)
\(E(5)\) и \(K(-17)\)

Для понимания важно знать какая из точек находится правее, а какая левее. Хотя это не важно, так как мы берем расстояние по модулю, то есть отрицательным значение не может быть.

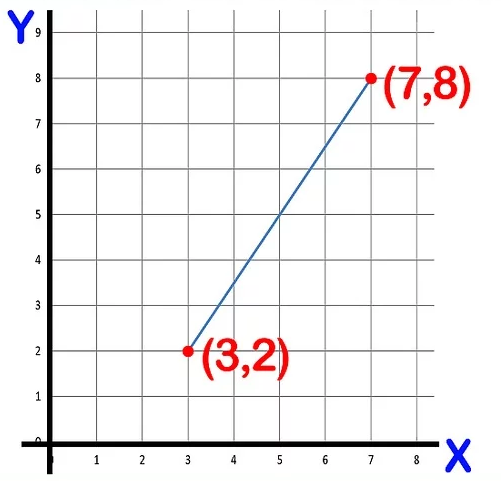
Решение:

\(|AB|=b-a\)

1) \(|AB| = 3-(-15)=|18|=18\)

2) \(|CD| = (3;2)-(7;8)=|(-4;-6)|=(4;6)-\) это означает на рисунке выше по оси x расстояние равно четырем единицам и по оси y 6 единицам длины.

3) \(|EK| = 5-(-17)=|22|=22\)

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Сложение и вычитание отрицательных дробей

Обновлено: 14 окт 2024

Периметр ромба

Обновлено: 16 авг 2024

Положительное и отрицательное направление угла

Обновлено: 16 июл 2024

Значения обратных тригонометрических функций y=arctg(x) и y=arcctg

Обновлено: 26 янв 2025

Функция обратной пропорциональности

Обновлено: 15 май 2024

О чем важно помнить, чтобы решать уравнения без труда

Обновлено: 04 ноя 2024

Учимся решать задачи по планиметрии

Обновлено: 17 сен 2024

ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)

Обновлено: 06 ноя 2024