ЕГЭ по математике, профильный уровень. Тригонометрическое уравнение
Условие:
а) Решите уравнение \(-{\sqrt2}sin(-{5π\over2}+x)*sinx=cosx\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \( [{9π\over2};6π\)]
Решение
а) Перед нами тригонометрическое уравнение, в котором имеются и синус, и косинус. Преобразуем сначала первое выражение синуса, содержащее аргумент в скобках. Так как синус является нечетной функцией, мы можем преобразовать исходное уравнение, избавившись от минуса перед выражением и поменяв знаки в скобке. Далее воспользуемся формулой приведения и еще более упростим начальное выражение:
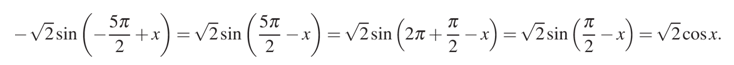
Запишем полученное выражение в наше уравнение и далее преобразуем к виду, когда выражение представляет произведение. Для этого перенесем правую часть уравнения влево и сгруппируем. После чего найдем корни:
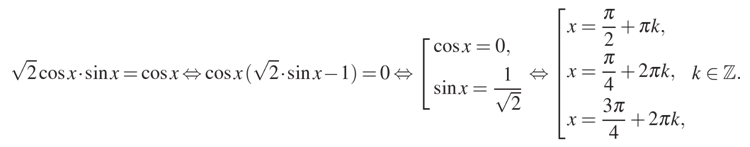
б) Отметим получившиеся корни на числовой прямой и найдем точки, входящие в искомый интервал [4,5π; 6π]
Мы получим следующие решения: 4,5π;4,75π;5,5π
Ответ:
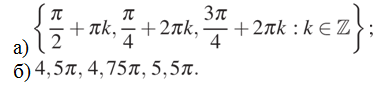
Автор - Андрей Найденов
Наши преподаватели
Репетитор по математике
Стаж (лет)
2
Образование:
Донецкий национальный университет
Проведенных занятий:
0
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов. Подготовка к ОГЭ, ЕГЭ, Я использую методы дискуссии, метод самостоятельной работы с учеником, метод самостоятельной работы с дидактическими материалами (для старших классов), анкетирование, презентация. Для меня химия - с детства любимый предмет. Было интересно познавать вещества, процессы происходящие с ними, самого себя. Я и сейчас считаю, что мой предмет важнейший, интереснейший. Без широкого знания в области химии невозможно сегодня развивать сельское хозяйство, здравоохранение, охрану природы, а значит, и общество в целом.
Репетитор по математике
Стаж (лет)
7
Образование:
Уфимский авиационный институт
Проведенных занятий:
8
Форма обучения:
Дистанционно (Скайп)
Повышение успеваемости по физике 7-11 класс, подготовка к ВПР, ОГЭ и ЕГЭ. Ответственно подхожу к делу, стараюсь объяснять законы физики на примерах из окружающего нас мира.
Репетитор по математике
Стаж (лет)
3
Образование:
Белорусский государственный университет
Проведенных занятий:
125
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов.
Я очень люблю математику, поскольку она блестяще развивает логическое мышление. Каждый раз, решая ту или иную нестандартную задачу, мне приходится осуществлять ее глубокий анализ, и найдя решение, при возможности я стараюсь найти 2-й, 3-й варианты решений и т.д. Такой подход позволяет преподавателю самому конструировать различные модели в голове и придумывать разносортные задачи на любую тему. Что же касается моей собственной методики обучения учащихся, то я стараюсь в работе периодически чередовать методы организации учебно-познавательной деятельности(словесные, наглядные, практические), методы стимулирования учебно-познавательной деятельности(дидактические игры, метод дискуссии), методы контроля за эффективностью учебно-познавательной деятельности(устный, письменный).Особо выделю такой метод как метод дискуссии. На мой взгляд, это очень эффективный метод , потому что в беседе на ту или иную математическую тему у учащегося развивается очень много навыков, что позволяет в дальнейшем совершать прогресс в рабочем процессе. Ученик должен выбрать именно меня, потому что я смогу его научить любить математику, нестандартно мыслить, решать задачи любого уровня, самому находить ошибки в решении (условии) задач и т.д.
Похожие статьи
- Вертикальные углы
- Признак делимости на 19
- ГМУ: Финансовый Университет при Правительстве Российской Федерации
- РУДН: факультет Психологии (отзывы,проходной балл, стоимость обучения)
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 5)
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 4)
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 5)
- Задачи на движение по окружности