Задачи с прикладным содержанием (вариант 2)
Предметы
Специализации
- Репетитор по геометрии
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор для подготовки к ОГЭ по физике
- Репетитор по русскому языку для подготовки к ЕГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор для подготовки к ВПР по английскому языку
- ВПР по физике
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор для подготовки к ОГЭ по обществознанию
- Репетитор по информатике для подготовки к ОГЭ
Задача №1
Наблюдатель находится на высоте «h», выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле:
L= \(√{{R•h}\over 500}\)
Где:
R - радиус Земли, R = 6400 км
С какой высоты горизонт виден на расстоянии 4 километров? Ответ выразите в метрах.
Решение
Задача сводится к решению уравнения:
L = 4
При заданном значении «R», получим:
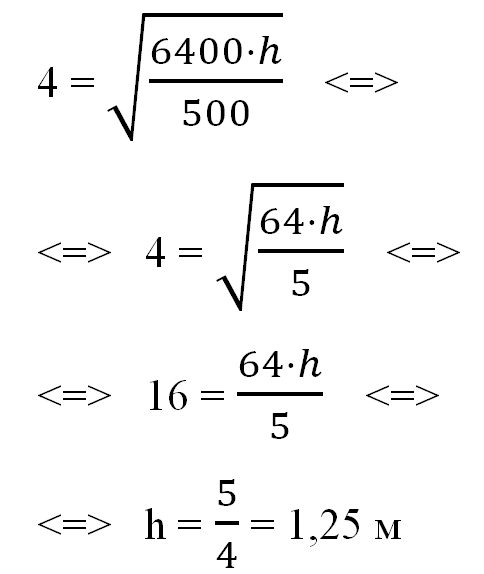
Ответ: 1,25.
Задача №2
Расстояние (в км) от наблюдателя, находящегося на высоте «h» м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле:
L = \(√{{R•h}\over 500}\)
Где:
R - радиус Земли, R = 6400 км
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
Решение
Задача сводится к решению уравнений:
L = 4,8
L = 6,4
При заданном значении «R», получим:
1)
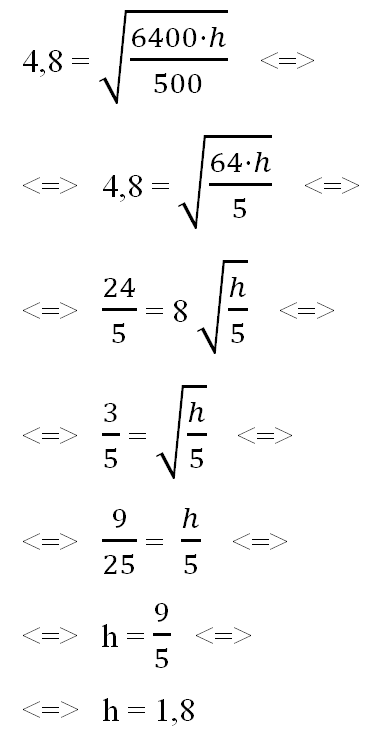
2)
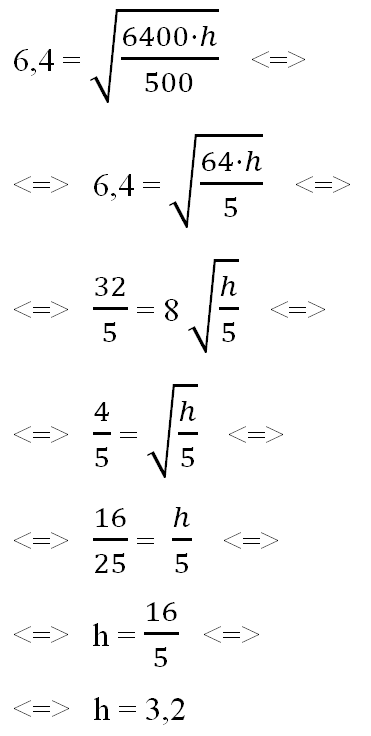
Следовательно, чтобы видеть горизонт на более далеком расстоянии, наблюдателю нужно подняться на высоту:
3,2 – 1,8 = 1,4 метра
Ответ: 1,4.
Наши преподаватели
Репетитор по математике
Стаж (лет)
4
Образование:
Московский государственный областной университет
Проведенных занятий:
1631
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
2
Образование:
Самаркандский Государственный Университет
Проведенных занятий:
293
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
24
Образование:
Гомельский государственный университет им. Ф. Скорины
Проведенных занятий:
1454
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Решение показательных уравнений
- Задачи на оптимизацию. Задание №17 из ЕГЭ
- Решаем задачи на движение по окружности
- Подходящие специальности для детей-интровертов
- 10 полезных перекусов для ученика между уроками
- Закаливание детей: мифы и реальность или почему нельзя сходу с головой в прорубь?
- Самые необычные животные на планете
- Переход в другую школу: как помочь ребенку справиться со стрессом и влиться в коллектив