Нахождение НОК И НОД чисел

 

Для начала вспомним, что такое простые числа – это числа, которые имеют два делителя: само себя и $1$. Давайте рассмотрим два числа $18$ и $48$ и найдем числа которые будут делится без остатка на них – $864$ и $144$. Наименьшее из них $144$, то есть мы нашли наименьшее общее кратное, сокращенно $НОК$. Когда мы вычисляем $НОК$ двух чисел, мы записываем их в круглых скобках $НОК$$(48;18).$ А если у нас очень большие числа, как нам тогда искать $НОК$? Для этого мы каждое число  должны разложить на простые множители. Взять множители разложения большего числа и недостающие из второго и перемножить их.

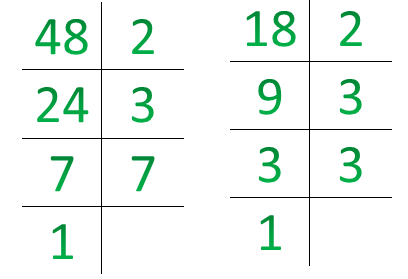
НОК$(48;18)=2*3*4*2*3=144.$

---

Давайте найдем $НОК$ у $7$ и $9$. Раскладываем на простые множители:

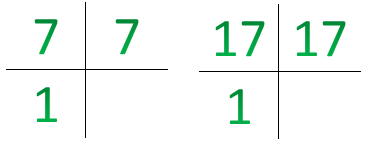
$7$ и $17$ – это простые числа, так как они делятся на себя и на $1$, то есть общий делитель у них $1$. Два числа называются взаимно простыми, если у них нет общих делителей, кроме числа $1$. Как же нам в этом случае найти $НОК$? Применяем все те же правила. Берем простые множители из наибольшего числа и недостающие из второго и затем перемножаем их.  $НОК$ чисел $17$ и $7$  равен их произведению, то есть $119$. Можно сформулировать простое правило для нахождения $НОК$ у взаимно простых чисел:

Чтобы найти $НОК$ у взаимно простых чисел, мы должны перемножить их. Легко, не так ли?

---

Задача 1. Найти $НОК$(840;140).

Раскладываем на простые множители:

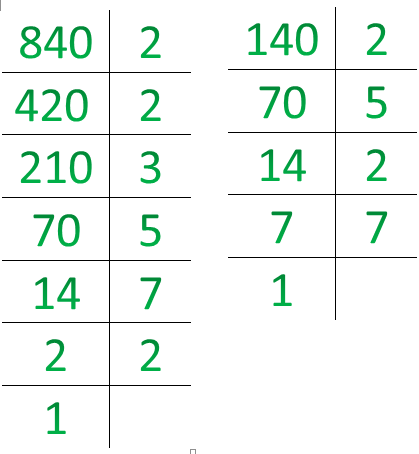
Заметив, что множители в числе $140$ повторяются, берем множители разложение большего числа: $2*2*3*5*7*2=840.$

Ответ: $НОК$$(840;140)=840.$

---

Далее введем понятие наибольшего общего делителя, сокращенно $НОД$. Для его нахождения нужно также разложить на простые сомножители и перемножить их общие цифры.

Задача 2. Найти $НОД$(840;140).

Решение. Выше можно посмотреть разложение этих чисел на простые множители.

Общие множители это 2*5*2*7=140.

Ответ: $НОД$(840;140)=140.