Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Задачи на движение по прямой (вариант 2)
Задача №1
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение
Пусть «V» км/ч – скорость второго пешехода, тогда скорость первого равна:
V + 1,5 км/ч
Пусть через «t» часов расстояние между пешеходами станет равным 0,3 километра. Таким образом, получим уравнение:
0,3 = (V + 1,5)·t – Vt <=>
<=> 0,3 = 1,5·t <=>
<=> t = 0,2
Получили:
t = 0,2 часа, или t = 12 минут
Ответ: 12.
Задача № 2
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Решение
Пусть «V» км/ч – скорость третьего велосипедиста.
А «t» часов – время, которое понадобилось ему, чтобы догнать второго велосипедиста.
Таким образом, получим:
Vt = 10·(t + 1) <=>
<=> V = \({(10•(t+1))} \over t\)
А через 2 часа 20 минут после этого догнал первого.
Таким образом, получим:
V·(t + \(7\over3\)) = 15·(t + \(7\over3\) + 2) <=>
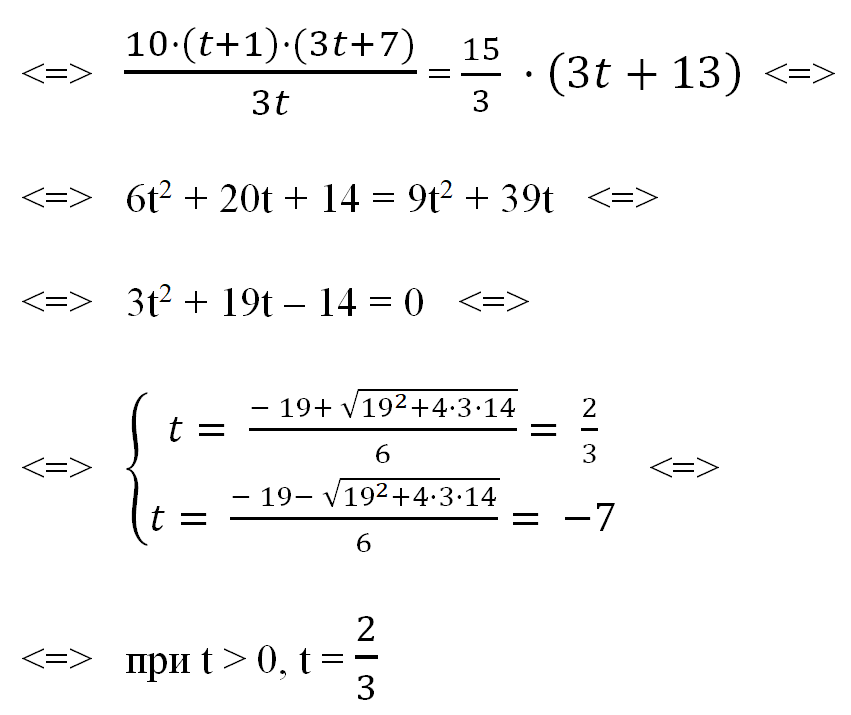
Таким образом:
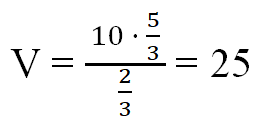
Ответ: 25.
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор по геометрии
Репетитор по геометрии -
 Подготовка к олимпиадам по химии
Подготовка к олимпиадам по химии -
 Подготовка к ЕГЭ по английскому онлайн
Подготовка к ЕГЭ по английскому онлайн -
 Репетитор для подготовки к олимпиаде по английскому
Репетитор для подготовки к олимпиаде по английскому -
 Репетитор ЕГЭ по обществознанию
Репетитор ЕГЭ по обществознанию -
 Репетитор по обществознанию ОГЭ
Репетитор по обществознанию ОГЭ -
 Подготовка к ЕГЭ по биологии онлайн
Подготовка к ЕГЭ по биологии онлайн -
 Подготовка к ЕГЭ по информатике
Подготовка к ЕГЭ по информатике -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

