Как построить график гиперболы?

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Что такое гипербола?
Формула гиперболы
Каковы особенности гиперболы?

Сегодня расскажем, как построить гиперболу, сколько точек нужно для гиперболы и что такое вообще гипербола.

Что такое гипербола?

Гипербола - это одна из классических кривых в геометрии. Она представляет собой геометрическое место точек, для которых разность расстояний до двух фокусов является постоянной. Гипербола имеет две ветви, которые стремятся к бесконечности вдоль своих асимптот. Она может быть ориентирована вертикально или горизонтально в зависимости от уравнения, описывающего её форму.

График гиперболы имеет вид \(y =\frac{k}{x}\) , где k-вещественное число и x ≠ 0. Также данную функцию называют обратной пропорциональностью, где \(k-\)коэффициент обратной пропорциональности.

Формула гиперболы

Как выглядит сам график в зависимости, стоит ли функция гиперболы с минусом или без перед \(x \):

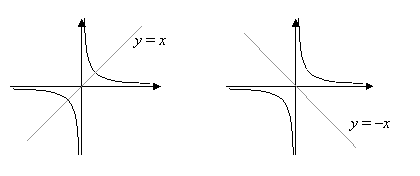
Каковы особенности гиперболы?

График \(y =\frac{k}{x}\) приближается к оси \(x \) по мере увеличения значения \(x \), но никогда не встречается с осью \(X\). Это называют горизонтальной асимптотой графика.

Каждая часть графика также становится ближе к оси \(y\), поскольку \(x \) приближается к \(0\), но никогда не встречается с осью \(y\), потому что нет значения для \(y\), когда \(x = 0\). Это называется вертикальной асимптотой графика.

Пример 1.

Построим график \(y =\frac{5}{x}\) на промежутке от \(4\) до \(4\), за исключением точки когда \(x = 0\). Выберем произвольное значение \(x \) и посчитаем соответствующее значение \(y\):

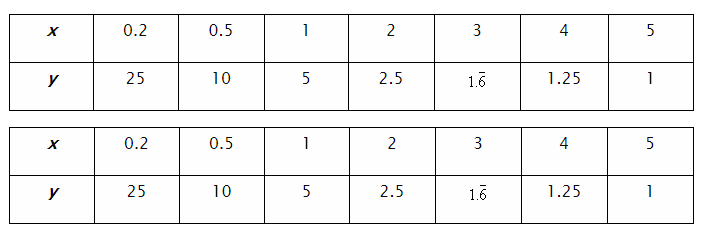
По высчитанным точка из таблицы построим график:

Часто задаваемые вопросы:

Часто задаваемые вопросы

Какие характеристики гиперболы нужно определить перед построением?

Прежде всего, определите положение центра гиперболы, длины ее полуосей и ориентацию (горизонтальную или вертикальную).

Что такое асимптоты гиперболы?

Асимптоты гиперболы - это прямые, которые графически приближаются к графику гиперболы по мере удаления от центра.

Как определить точки для построения графика гиперболы?

Определите несколько точек на графике, используя значения координат из уравнения гиперболы, затем нарисуйте график, соединив эти точки с учетом формы и ориентации гиперболы.

Предыдущая статья