img
О платформе Новое Премиум математика Репетиторы Тарифы
Записаться на урок

Дарим первый урок с репетитором бесплатно

Оставьте заявку и получите первый урок в подарок

bg bg gift

Задачи с логарифмическими уравнениями и неравенствами

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 21 фев 2024

Задачи с логарифмическими уравнениями и неравенствами

 
Задача №1
 
Ёмкость высоковольтного конденсатора в телевизоре равна:
 
С = 2·10-6 Ф
 
Параллельно с конденсатором подключeн резистор с сопротивлением:
 
R = 5·106 Ом
 
Во время работы телевизора напряжение на конденсаторе равно:
 
U0 = 16 кВ
 
После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением:
 
t = \(αRC•log_2 {U_2\over U}\)
 
Где:
\(α\) – постоянная, \(α\) = 0,7
 
Определите напряжение на конденсаторе, если после выключения телевизора прошло 21 с. Ответ дайте в киловольтах.
 
Решение
 
Задача сводится к решению неравенства:
 
t \(≥\) 21
 
При заданных значениях начального напряжения на конденсаторе, сопротивления резистора и ёмкости конденсатора, получаем:
 
t \(≥\) 21   <=>
 
<=>   0,7·2·10-6·5·106·log2 \(16\over U\) \(≥\)  21   <=>
 
<=>   log2 \(16\over U\)  \(≥\) 3  <=>
 
<=>  \(16\over U\) \(≥\)  8  <=>
 
U \(≤\) 2 кВ
 
Ответ: 2.
 
Задача № 2
 
Для обогрева помещения, температура в котором поддерживается на уровне:
 
Тп = 20 ºС
 
Через радиатор отопления пропускают горячую воду. Расход проходящей через трубу воды:
 
m = 0,3 кг/с
 
Проходя по трубе расстояние «х», вода охлаждается от начальной температуры:
 
Тв = 60 ºС
 
до температуры Т(ºС), причeм:
 
 
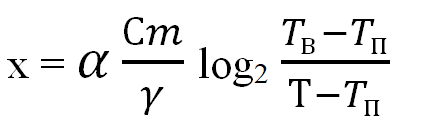
Где:
С - теплоeмкость воды, С = 4200 \(Дж/(кг•ºС)\)
\(γ\) - коэффициент теплообмена, \(γ\) = 21\(Вт/(м•ºС)\)
\(α \) – постоянная, \(α \) = 0,7
 
Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.
 
Решение
 
Задача сводится к решению уравнения:
 
 
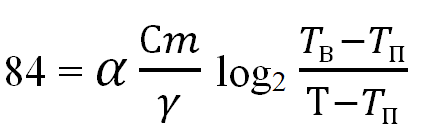
При заданных значениях теплоёмкости воды, коэффициента теплообмена, постоянной, температуры помещения и расхода воды, получим:
 
 
 
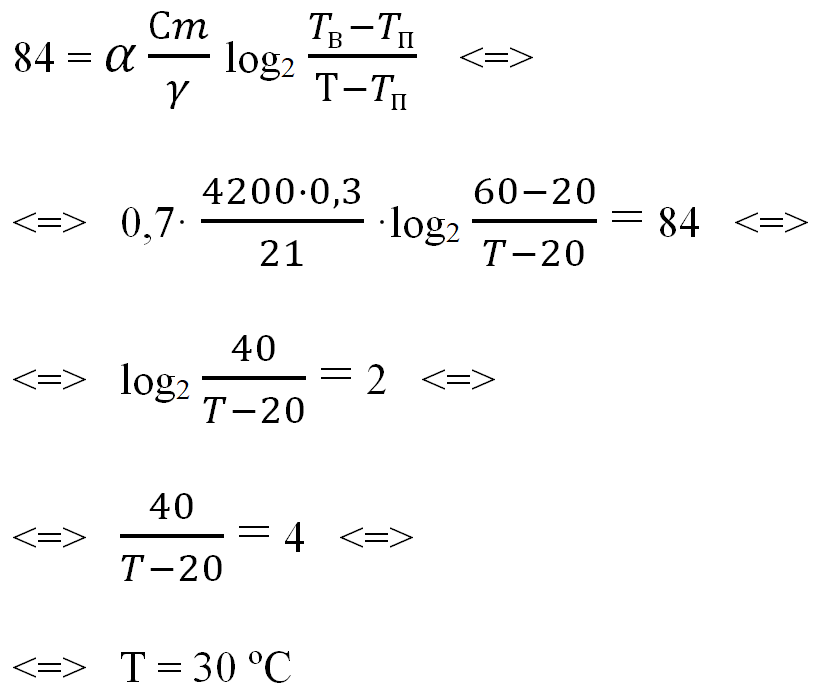
Ответ: 30.
 
Предыдущая статья img Следующая статья img

Дарим в подарок бесплатный вводный урок!

line gift
Репетиторы arrow
Специализация arrow

Похожие статьи

img

Высшая Школа Бизнес-информатики (НИУ ВШЭ)

Обновлено: 22 июл 2024

 img

РУДН: Нефтегазовое дело (вступительные испытания, отзывы)

Обновлено: 06 июн 2024

 img

ЕГЭ по математике, профильный уровень. Задача с параметром

Обновлено: 14 апр 2024

 img

Задача на растворы

Обновлено: 02 авг 2024

 img

ЕГЭ по математике, базовый уровень. Задачи на числовые ряды и прогрессии

Обновлено: 24 апр 2024

 img

Нужна ли вашему ребенку ментальная арифметика?

Обновлено: 29 дек 2023

 img

Подборка логических задач для школьников 3-4 класса

Обновлено: 10 июл 2024

 img

Обучение во вторую смену: плюсы и минусы, как помочь ребенку адаптироваться

Обновлено: 14 май 2024