Задачи на исследование функций
Предметы
Специализации
- Репетитор по алгебре
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор по химии для подготовки к ОГЭ
- Подготовка к олимпиадам по химии
- Репетитор для подготовки к ОГЭ по физике
- Репетитор по английскому языку для подготовки к ОГЭ
- Репетитор по английскому для взрослых
- Репетитор для подготовки к ВПР по русскому языку
- ВПР по физике
- Репетитор по информатике для подготовки к ОГЭ
Задача №1
Найдите наименьшее значение функции:
у = х3 – 27·х
на отрезке [0;4]
Решение
Найдем производную заданной функции:
у' = 3х2 – 27 = 3(х2 – 9) = 3(х – 3)(х + 3)
Найдем нули производной:
3(х – 3)(х + 3) <=>
0 \(≤\) х \(≤\) 4
х1 = -3
х2 = 3
Определим знаки производной функции и изобразим на рисунке (Рис.1) поведение функции:
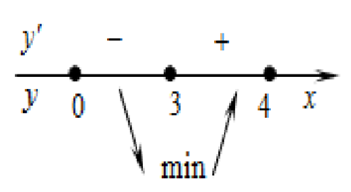
Рис.1
В точке х = 3 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
y=(3) = 27 - 27·3 = - 54
Ответ: −54.
Задача №2
Найдите наибольшее значение функции:
у = х3 – 3·х + 4
на отрезке [-2;0]
Решение
Найдем производную заданной функции:
у' = 3х2 – 3 = 3(х2 – 1) = 3(х – 1)(х + 1)
Найдем нули производной:
3(х – 1)(х + 1) <=>
- 2 \(≤\) х \(≤\) 0
х1 = -1
х2 = 1
Определим знаки производной функции и изобразим на рисунке (Рис.2) поведение функции:
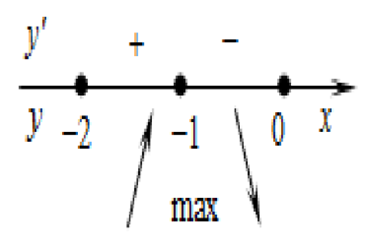
Рис.2
В точке х = -1 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
у(-1) = -1 + 3 + 4 = 6
Ответ: 6.
Задача №3
Найдите наименьшее значение функции:
у = 9х2 – х3
на отрезке [-1;5]
Решение
Найдем производную заданной функции:
у' = 18х – 3х2 = 3х(6 - х)
Найдем нули производной:
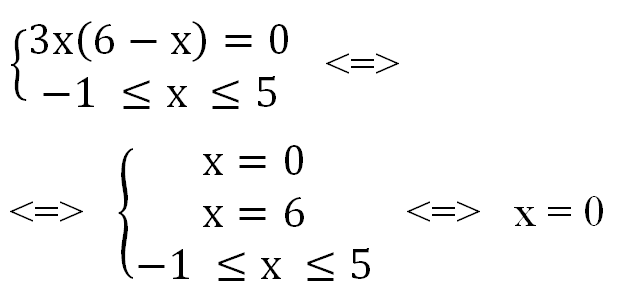
Определим знаки производной функции и изобразим на рисунке (Рис.1) поведение функции:
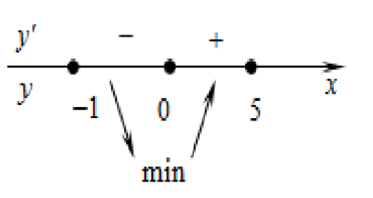
Рис.1
В точке х = 0 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
у(0) = 9 · 02 – 03 = 0
Ответ: 0.
Задача №4
Найдите наибольшее значение функции:
у = 9х2 – х3
на отрезке [2;10]
Решение
Найдем производную заданной функции:
у' = 18х – 3х2 = 3х(6 - х)
Найдем нули производной:
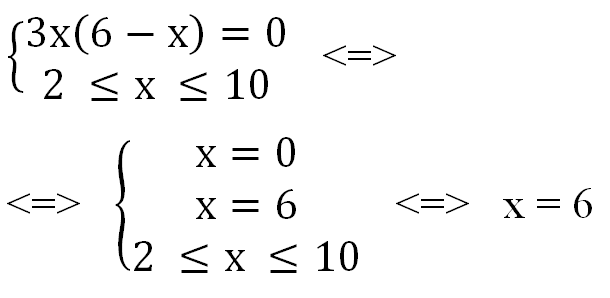
Определим знаки производной функции и изобразим на рисунке (Рис.2) поведение функции:
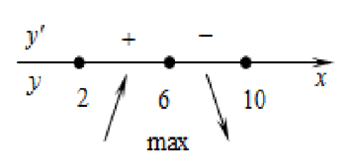
Рис.2
В точке х = 6 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
у(6) = 9 · 62 – 63 = 324 – 216 = 108
Ответ: 108.
Задача №5
Найдите точку максимума функции:
у = х3 – 5х2 + 7х – 5
Решение
Найдем производную заданной функции:
у' = 3х2 – 10х + 7
Найдем нули производной:
3х2 – 10х + 7 = 0
х1 = 1
х2 = \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)![]()
![]( "Нажмите и перетащите")
Определим знаки производной функции и изобразим на рисунке (Рис.1) поведение функции:
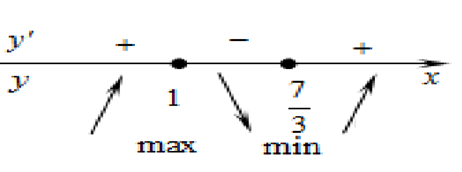
Рис.1
Искомая точка максимума х = 1
Ответ: 1.
Задача №6
Найдите точку минимума функции:
у = х3 + 5х2 + 7х – 5
Решение
Найдем производную заданной функции:
у' = 3х2 + 10х + 7
Найдем нули производной:
3х2 + 10х + 7 = 0
х1 = -1
х2 = \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)![]()
![]( "Нажмите и перетащите")
Определим знаки производной функции и изобразим на рисунке (Рис.2) поведение функции:
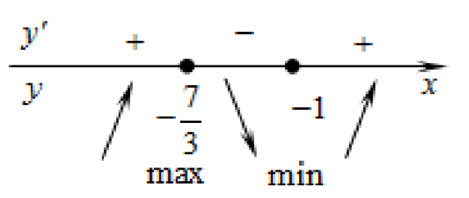
Рис.2
Искомая точка минимума х = -1
Ответ: −1.
Часто задаваемые вопросы:
✅ Что такое задачи на исследование функций?
↪ Задачи на исследование функций - это математические задачи, которые требуют анализа и понимания свойств функций, включая определение области определения и области значений, анализ поведения функции на промежутках, точки разрыва, асимптоты и экстремумы.
✅ Каковы шаги исследования функции на область определения?
↪ 1) Определение всех значений "x", при которых функция имеет смысл и не является неопределенной. 2) Исключение значений "x", которые приводят к делению на ноль или извлечению отрицательного числа под корнем.
✅ Как найти точки разрыва функции?
↪ Точки разрыва функции возникают, когда функция не является непрерывной в какой-то точке "x". Такие точки можно найти, исследуя значение функции в окрестности возможных разрывов.
Наши преподаватели
Репетитор по математике
Стаж (лет)
10
Образование:
Столичный центр переподготовки г. Москвы
Проведенных занятий:
35
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
4
Образование:
Университет штата Аризона
Проведенных занятий:
1095
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
14
Образование:
Кишинёвский ордена Трудового Красного знамени государственный университет имени В.И.Ленина
Проведенных занятий:
305
Форма обучения:
Дистанционно (Скайп)