Уравнения смешанного типа
Условие:
а) Решите уравнение ![]()
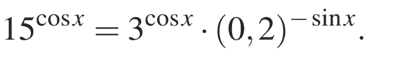
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решение
а) В нашем случае – это показательное уравнение, в котором в показателе степени стоит тригонометрическая функция. Преобразуем уравнение и решим его.
Основание степени «15», стоящее в левой части, преобразуем в произведение: 15 = 3 х 5
Тогда запишем и раскроем скобки:
(3 х 5)cos x = 3cos x х 5cos x
В правой части преобразуем:
0,2 = 1/5 = 5-1
Тогда мы сможем записать:
(5-1)-sin x = 5sin x
Сократим обе части уравнения на «3cos x», при условии, что «3cos x > 0»
В полученном уравнении разделим обе части на «cos x» и найдем корни.
Запишем весь ход решения:
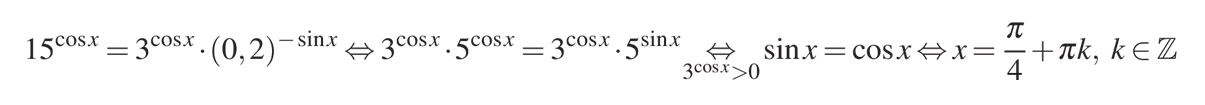
б) Отберем те корни уравнения, которые принадлежат отрезку
Получим корни: 
Ответ: 
Автор - Андрей Найденов
Наши преподаватели
Репетитор по математике
Стаж (лет)
21
Образование:
Могилевский государственный университет им А.А. Кулешова
Проведенных занятий:
1208
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов. Занимаюсь подготовкой к сдаче ОГЭ, ЕГЭ. В преподавании считаю самым главным комфортную атмосферу и доверие. Помогаю ученикам не бояться ошибок. Считаю, что умение помочь ученику поверить в свои силы, увидеть свой потенциал - это миссия каждого учителя!
Репетитор по математике
Стаж (лет)
5
Образование:
Ульяновский государственный педагогический университет имени ИН Ульянова
Проведенных занятий:
0
Форма обучения:
Дистанционно (Скайп)
Я считаю, что знать русский язык, грамотно писать и говорить на нём – это гражданский долг каждого человека, проживающего в Российской Федерации. Тем самым мы проявляем уважение к языку и сохраняем его для будущих поколений.
Беру в работу как начальные, так и средние классы; осуществляю подготовку детей в ВПР, ОГЭ, олимпиадам, проектам; даю консультации.
Методы преподавания, которые используются в работе с учеником, направлены на определение целей и задач обучения русскому языку как родному и их результативность.
Репетитор по математике
Стаж (лет)
27
Образование:
БГУ , Институт Позитивных Технологий и Консалтинга
Проведенных занятий:
1806
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 класса. Активно использую в своей работе не только знания математики., но и навыки консультанта-психолога, объединяя их для достижения желаемого результата. Искренне считаю, что без позитивного контакта с учеником, на возможен полноценный процесс обучения! Математику люблю, как предмет! Уважаю, как науку! И с удовольствием этим делюсь на своих занятиях.
Похожие статьи
- Как легко умножить на 0,25
- Графики кубических функций
- Как решать логарифмические уравнения
- Факультет Менеджмента (НИУ ВШЭ)
- РУДН: Ландшафтная Архитектура
- ЕГЭ по математике, профильный уровень. Рациональные уравнения
- Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость). Формула Ньютона-Лейбница
- Необычные профессии мира