Арифметическая прогрессия

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 08 апр 2024

Арифметическая прогрессия

Теория вопроса

Арифметическая прогрессия - это бесконечная последовательность чисел, записанная в виде:

a1, a2, ..., an, …

где а1 - первый член,

а2 - второй член,

аn - "энный" член прогрессии,

каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d ≠ 0

число d – это "шаг" или "разность" прогрессии.

Если постоянное число d > 0, то прогрессия называется возрастающей.

Если постоянное число d < 0, то прогрессия называется убывающей.

Любой член арифметической прогрессии вычисляется по формуле:

a_n = a₁ + d ( n – 1 ) .

Сумма "n" первых членов арифметической прогрессии вычисляется как:

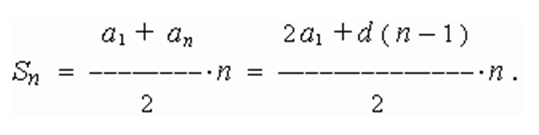
Приведем примеры задач, где необходимо использовать эти формулы.

Задача

Найти сумму первых ста нечётных чисел. Найти нечетное число, которое занимает 45-е место в этом списке.

Решение

1) Нечетными числами является множество, состоящее из следующих членов: 1, 3, 5, 7, 9, 11, 13, …

В задаче просят найти сумму первых ста чисел этой последовательности. Удобно эту последовательность определить как арифметическую. При этом получится, что первый член: a₁ = 1, а разность прогрессии: d = 2.

Применим формулу для нахождения суммы "n" первых членов этой прогрессии, где n = 100:

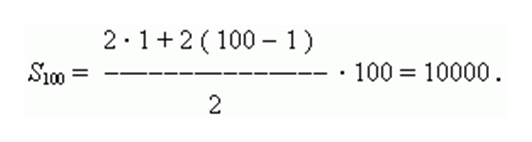
2) Чтобы найти 45-й член последовательности, применим формулу для вычисления "энного" члена последовательности, где n = 45:

а(45) = 1 + 2(45 – 1) = 1 + 2 х 44 = 1 + 88 = 89

Как видите, применение формул значительно ускоряет нахождение и суммы первых членов арифметической последовательности, и одного из членов этой последовательности.

Автор - Андрей Найденов

Предыдущая статья