Определение неопределенного интеграла

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

История открытия интегралов
Где используют интегралы?
Часто задаваемые вопросы:

Обновлено: 23 фев 2024

Определение неопределенного интеграла

Неопределенный интеграл — это понятие из математического анализа, которое используется для нахождения первообразной (антипроизводной) функции. В этой статье расскажем, что такое неопределенный интеграл и как его можно использовать.

Неопределенный интеграл - это обратная операция к дифференцированию. Когда мы дифференцируем функцию, мы находим ее производную, которая показывает, как быстро изменяется функция в каждой точке. Неопределенный интеграл, наоборот, позволяет найти функцию, производная которой равна исходной функции.

Интеграл является важной частью дифференциального исчисления. Интегралы могут быть двойные, тройные и т.д. Для нахождения площади поверхности и объема геометрических тел используются различные типы интегралов.

Неопределенный интеграл имеет вид: \(∫f (x)\, dx\) и определенный интеграл имеет вид: \(\int_a^b \! f (x)\, dx\)

Область плоскости, ограниченной графиком определенный интеграла:

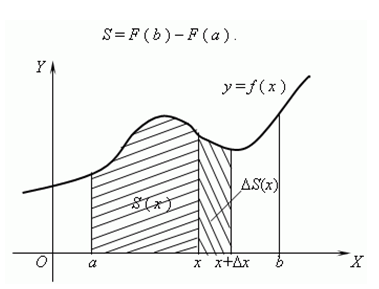
Операция интегрирования обратна операции дифференцирования. По этой причине надо вспомнить первообразную, функцию, таблицу производных .

Функция \( F (x) = x^2\) является первообразной для функции \(f ( х ) = 2х\). Функции \(f ( х ) = x^2+2\) и \(f ( х ) = x^2+7\) также является первообразными для функции \(f ( х ) = 2х\). \(2\) и \(7-\) это константы, производные которых равны нулю, поэтому мы можем подставлять их сколько угодно, значение первообразной не изменится. Для записи неопределенного интеграла использует знак \( ∫\). Неопределенный интеграл - это совокупность всех первообразных функции \(f ( х ) = 2х\). Операции интегрирования обратны дифференцированию. \(∫2x = x^2+C\), где \(C\) это константа интегрирования, то есть если мы вычислим производную \(x^2\), то получим \(2x\), а это и есть \( ∫2x\). Легко, не правда ли? Если вы не поняли, то вам надо повторить производную функции. Теперь мы можем вывести формулу по которой мы будем вычислять интеграл: \(∫u^ndu=\frac{u^n+1} {n+1}, n ≠ -1\). мы вычитали 1, теперь мы прибавляем 1 , n не может быть равно 0.

Также существуют другие правила интегрирования для других основных функций которые надо выучить. Таблица интегралов поможет вам выучить все основные формулы интегралов:

Решение неопределенного интеграла это обратный процесс нахождения первообразных дифференциального уравнения. Мы находим функцию, производная которой является интегралом, и не забываем добавлять "+ C" в конце.

История открытия интегралов

Принципы интегрального исчисления были сформулированы независимо друг от друга Исааком Ньютоном и Готфридом Лейбницем в конце 17-го века. Бернхард Риман дал строгое математическое определение интегралов. Первым документированным систематическим методом, способным определять интегралы, является метод исчисления древнегреческого астронома Евдокса, который пытался найти площади и объемы, разбив их на бесконечное число известных площадей и объемов. Этот метод был далее разработан и использован Архимедом в 3-м веке до н. э. и использовался для расчета площадей парабол и приближения к площади круга.

Аналогичный метод был независимо разработан в Китае около 3-го века нашей эры Лю Хуэем, который использовал его, чтобы найти площадь круга. Этот метод позже был использован в 5-м веке китайскими математиками — отцом и сыном ЗУ Чунчжи и ЗУ Генгом, чтобы найти объем сферы.

Следующие значимые достижения в интегральном исчислении не появлялись до 17-го века. В это время работы Кавальери и Ферма начали закладывать основы современного исчисления.

В частности, фундаментальная теорема исчисления интегралов позволяет решать гораздо более широкий класс задач. Равным по важности является комплексная математическая структура, которую разработали Ньютон и Лейбниц. Эта структура интегралов взята непосредственно из работы Лейбница и стала современным интегральным исчислением. Исчисление было изменено Риманом, используя пределы. Впоследствии были рассмотрены более общие функции, особенно в контексте анализа Фурье, к которым определение Римана не применяется. Лебег сформулировал другое определение интеграла, основанное в теории мер (подполе реального анализа).

Современное обозначение неопределенного интеграла было введено Готфридом Лейбницем в 1675 году.

Где используют интегралы?

Интегралы широко используются во многих областях математики. Например, в теории вероятностей интегралы используются для определения вероятности попадания некоторой случайной величины в определенный диапазон.

Интегралы могут быть использованы для вычисления площади двумерной области, имеющей криволинейную границу, а также для вычисления объема трехмерного объекта, имеющего криволинейную границу.

Интегралы используются в физике, в таких областях, как кинематика, чтобы найти перемещение, время и скорость.

Часто задаваемые вопросы:

✅ Что такое неопределенный интеграл?

↪ Неопределенный интеграл - это обратная операция к дифференцированию, которая позволяет найти функцию, производная которой равна исходной функции.

✅ Как обозначается неопределенный интеграл?

↪ Символически неопределенный интеграл обозначается как ∫f(x) dx, где "f(x)" - подынтегральная функция, а "dx" - обозначение переменной, по которой мы интегрируем.

✅ Как найти неопределенный интеграл функции?

↪ Для нахождения неопределенного интеграла мы применяем правила и методы интегрирования, в основном используя обратные операции к правилам дифференцирования, чтобы найти функцию, производная которой равна исходной функции.

Предыдущая статья