Модуль числа (Часть 1)

Дарим в подарок бесплатный вводный урок!

Предметы
Специализации
В этой статье мы обсудим наиболее непонятную для многих тему модуль числа, научимся решать неравенства, связанные с абсолютными значениями.

Что такое модуль числа?

Модуль числа - это его абсолютное значение (отрицательное или положительное значение)  обозначается как  \(|a |\) :
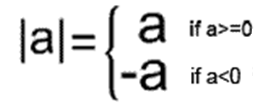
  \(|5 | =5 \) если \(5>0 \)
  \(|-\frac{4}{7}|= -(-\frac{4}{7}) = \frac{4}{7}\) если \(-\frac{4}{7}<0 \)
  \( |0|=0\), так как \( 0≥0 \)

 Пример 1. \(|x-3 |=4\)
Решение :
  \(x-3= 4 \)      \(-(х-3)= 4\)
        \( х= 7 \)        \( x-3= -4 \)
                          \( x= -1\)
Ответ: \( х= 7 \) ; \( x= -1\)
         
 Пример 2. Решить \( |3x-2 | = |5x+4| \)
Решение:
                                                                                        \( |3x-2 | = |5x+4| \)                \(3x-2 = - (5x+4)\)
                                                                                         \(3x-5x = 4+2\)                     \(x=-\frac{1}{4}\)
                                                                                         \( - 2x = 6\)
                                                                                          \( x = -3 \)
                                                                                           Ответ: \( x = -3 \) ; \(x=-\frac{1}{4}\)
    Продолжение статьи Модуль числа (Часть 2)
    
Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Михаил Николаевич Макеев
Репетитор по математике
Стаж (лет)
9
Образование:
Московский энергетический институт
Проведенных занятий:
755
Форма обучения:
Дистанционно (Скайп)
Татьяна Сергеевна Вахнина
Репетитор по математике
Стаж (лет)
23
Образование:
Орский государственный педагогический институт
Проведенных занятий:
934
Форма обучения:
Дистанционно (Скайп)
Анна Михайловна Глущенко
Репетитор по математике
Стаж (лет)
23
Образование:
Восточная экономико-юридическая гуманитарная академия
Проведенных занятий:
645
Форма обучения:
Дистанционно (Скайп)
Похожие статьи