Неравенства с модулем

Как решать неравенства с модулем?
Методы решения систем линейных неравенств отличаются от методов решения линейных уравнений тем, что знаки неравенства не позволяют выполнять подстановку, как мы это делаем с уравнениями. Тем не менее, мы решаем по определенной системе. Система линейных неравенств включает в себя несколько выражений, которые при решении могут дать ряд решений.
Неравенства с модулем
 
\(|x|\)— расстояние на числовой прямой от  \(0\) до точки \(a\).
  1. \(|u|=u\) \(-->\) \(u\geq0\)
  2. \(|u|=-u\) \(-->\) \(u\le \: 0\)
  3. \(|u|=|v|\)     \(-->\) \(v^2=u^2\)
  4. \(|x|<a \)  \(-->\)  \(-a<x<a\)    Система
  5. \(|x|\le \:a \) \(-->\)  \(-a\le \:x\le \:a\)  
  6. \(|x|> a \) \(-->\) \(\left[ \begin{gathered} x < -a \\ x >a \\ \end{gathered} \right.\)  Совокупность
  7. \(|x|\geq a \) \(-->\) \(\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.\)  
 
Пример 1. Решить неравенство  \(|3+x| \geq|x|\). 
Решение.  \(|3+x| \geq|x|\)\(-->\) \((3+x)^2\geq x^2\) \(-->\) \(x^2+6x+9\geq x^2\)  \(-->\) \(6x\geq -9\) \(-->\) \(x\geq -1,5\)
Неравенства с модулем
Ответ: \([-1,5; +∞)\)
Пример 2. Решить неравенство \(\left|3+2x\right|\le \:7\).  Система
Решение.  \(\left|3+2x\right|\le \:7\)     \(-->\)    \(3+2x\le \:7\) и  \(3+2x\ge \:-7\)  или  \(-7\le \:3+2x\le \:7\)
                                                          \(x\le \:2\)         и   \(x\ge \:-5\)                       \(-5\le \:x\le \:2\)
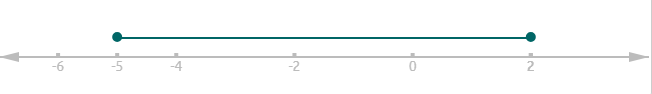
Ответ: [-5;2];
  Пример 3. Решить неравенство \(\left|3x-5\right|<\:4\)
Решение:         \(-4<3x-5<4\)  \(-->\) \(\frac{1}{3}<x<3\)
   Неравенства с модулем
                         
Ответ: \((\frac{1}{3};3)\);
Пример 4. Решить неравенство \(\left|x-8\right|\ge \:\:3\)
Решение: Совокупность  \(\) \(\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.\)  \(-->\) \(\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.\)
Неравенства с модулем
Ответ: \((+∞;5)⋃ (11;+∞)\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Андрей Алексеевич Тарасов
Репетитор по математике
Стаж (лет)
4
Образование:
Новосибирский государственный университет
Проведенных занятий:
86
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов, ВПР/ОГЭ/ЕГЭ, и по физике 6-9 классы ВПР/ОГЭ. Убежден, что математику может понять каждый человек. Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно! С нетерпением жду всех на занятиях!
Юлия Анатольевна Шустова
Репетитор по математике
Стаж (лет)
1
Образование:
Тюменский государственный университет
Проведенных занятий:
1
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов. Приветствую всех желающих изучать химию - науку о веществах и превращениях! Однажды открыв для себя этот волшебный мир, вы захотите снова и снова узнавать его тайны. Я с удовольствием сделаю для вас эту науку простой и понятной , покажу ученику, что мир химии очень интересен и увлекателен!
Анастасия Сергеевна Черная
Репетитор по математике
Стаж (лет)
2
Образование:
Кубанский Государственный Университет
Проведенных занятий:
220
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов. Подготовка к ОГЭ, ЕГЭ (базовый и профильный). Люблю математику за то, что она развивает аналитическое и критическое мышление Системно-деятельностный подход Информационно-развивающий и репродуктивный методы Подробное и доступное объяснение, уважительное отношение, индивидуальный подход Умею находить подход к ученикам любого уровня подготовки.
Похожие статьи