Вписанный угол окружности

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Чтобы понять, что такое вписанный угол, вспомним про круг и окружность.

Круг — очень важная геометрическая фигура, которая часто встречается в геометрии. Существует ряд понятий и теорем, связанных с кругом. Круг может образовывать множество различных типов углов внутри него, вписанный угол является одним из них. Этот угол образован двумя хордами и вершиной в круге. В треугольнике ABC вписанный угол образуется двумя лучами и вершиной на окружности. Пример \(∠APB\) — вписанный угол в окружность:

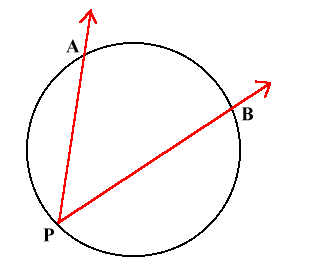
Мера вписанного угла равна половине измерения его дуги, то есть равна половине дуги \(AB\):
\( APB=84/2 = 42\)

Два вписанных угла, опирающихся на одну и ту же дугу, будут равны:

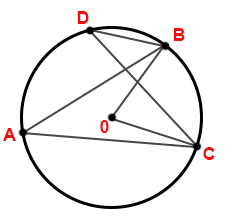
\(∠ BAC = ∠BDC\), так как опираются на одну и ту же дугу.

\(∠ CAB = \frac{1}{2} ∠BOC\)

\(∠ CDB =\frac{1}{2} ∠ BOC\)

Если мы знаем длину малой дуги и радиус, то величина вписанного угла вычисляется по формуле:

\(∠ X= \frac{ 90*Lπ}{R}\)

Часто задаваемые вопросы

Каково свойство вписанных углов в окружности?

Основное свойство вписанных углов заключается в том, что угол, подразумевающий дугу между двумя сторонами, равен половине центрального угла, опирающегося на ту же дугу.

Что такое центральный угол в окружности?

Центральный угол в окружности - это угол, который вершина которого находится в центре окружности и стороны проходят через точки окружности.

Какие единицы измерения используются для меры углов в окружности?

Мера углов в окружности обычно выражается в градусах (°), радианах (rad) или градусах, минутах и секундах (° ' ").

Предыдущая статья