Первообразная

Дарим в подарок бесплатный вводный урок!

Предметы

Специализации

Первообразная играет важную роль в математике и находит применение в различных областях, включая физику и экономику. Она помогает нам решать задачи, связанные с вычислением площадей, нахождением средних значений, решением дифференциальных уравнений и многим другим.

Что такое первообразная

Перед тем как выяснять, что такое первообразная функции, повторим, что такое функция:

Функция – это зависимость одной переменной (у) от другой(х), когда для каждого значения независимой переменной (х) из множества $Х$ (у) из множества Y.

Теперь определение первообразной:

Первообразная — это функция, которую мы дифференцируем, чтобы получить исходную функцию.

Как найти первообразную

Операция нахождения первообразной – это обратная операции нахождения производной. Первообразная для функции $ F (x) = 2x$ — это функция $f ( х ) = x^2$:

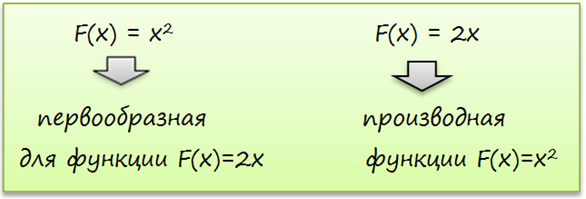
Первообразная для функции $ F (x) = 3x^2$ есть функция $f ( х ) = x^3$ для любого х ∈ R.

Первообразная для функции $f(x) = 2х$ есть функция $F(x) = x^2$ для любого $х ∈ R$. Функция $f ( х ) = x^3$ является первообразной для функции $ F (x) = 3x^2$.

Функции $f ( х ) = x^3+5$ и $f ( х ) = x^3+3$ также является первообразными для функции $ F (x) = 3x^2$. $3$ и $5$ — это константы, производные которых равны нулю, поэтому мы можем подставлять их сколько угодно, значение первообразной не изменится.

Семейством первообразных функции $ F (x) = 3x^2$ являются функции $f ( х ) = x^3+C$, где $C$ является константой.

Функция $F(x)$ называется первообразной для функции $f(x)$ на некотором промежутке $X$, если для каждого $х ∈ Х$ выполняется $F′(x) = f( x )$.

Выделим это определение:

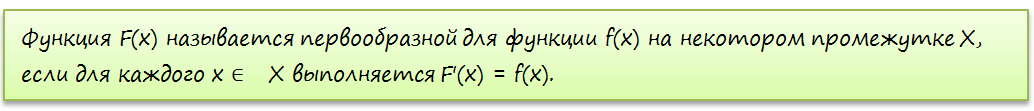
Термин “первообразная” означает площадь, ограниченную кривой функций. Изобразим графически производную $y = x^2:$

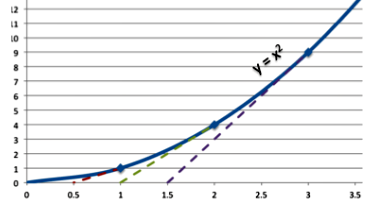
Касательные линии нарисованы пунктирными линиями в трех различных точках.

Заметим, что уклон в два раза больше значения переменной $x$ , то есть производная функции $y = х^2$ равна $ у=2х.$

Теперь рассмотрим функцию $y = 2x $:

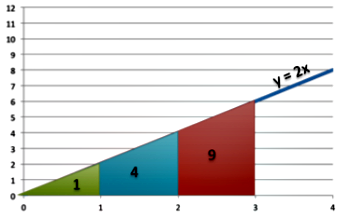
Рассмотрим площади треугольников под графиком $y = 2x.$

Площадь треугольника равна площади $\frac{1}{2}$ основания на высоту. Таким образом, ясно, что области под графиком:

$S_{1} = \frac{1}{2} \times 1 \times 2 = 1$

$S_{2} = \frac{1}{2} \times 2 \times 4 = 4$

$S_{3} = \frac{1}{2} \times 3 \times 6= 9$

Можно сказать, что первообразная эквивалентна площади под функцией.

Функция может иметь несколько первообразных.

$F(x)+C;$

Докажем что функция может иметь несколько первообразных:

$(F(x)+C) ′ =F ′ (x)+(C) ′ =f(x)+0=f(x).$

$(F(x)+C) ′ =f(x).$

Часто задаваемые вопросы:

✅ Что такое первообразная функции?

↪ Первообразная функции - это функция, производная которой равна исходной функции. Математически записывается как ∫ f(x) dx = F(x) + C, где F(x) - первообразная функции f(x), dx - символ дифференциала, а C - произвольная постоянная.

✅ Зачем нужна первообразная функция?

↪ Первообразная функция играет важную роль в теории интегралов. Она позволяет нам вычислять определенные интегралы, находить площади под кривыми, находить средние значения функций, решать дифференциальные уравнения и многое другое.

✅ Как найти первообразную функции?

↪ Нахождение первообразной функции называется интегрированием. Существует набор правил и методов для интегрирования различных функций. Некоторые из них включают применение формул интегрирования, методы замены переменной и интегрирование по частям. Выбор правильного метода зависит от конкретной функции, которую нужно проинтегрировать.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Татьяна Дмитриевна Макарова

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университ имени Максима Танка

Проведенных занятий:

317

Форма обучения:

Дистанционно (Скайп)

Жанна Игоревна Стефанович

Репетитор по математике

Стаж (лет)

Образование:

Гродненский государственный университет им. Янки Купалы

Проведенных занятий:

116

Форма обучения:

Дистанционно (Скайп)

Полина Андреевна Галямова

Репетитор по математике

Стаж (лет)

Образование:

ФГБОУ ВО

Проведенных занятий:

361

Форма обучения:

Дистанционно (Скайп)