Синус, косинус острого угла треугольника

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

19 сен 2024

Синус, косинус острого угла треугольника

Как найти синус и косинус угла в прямоугольном треугольнике? Для этого нужно вспомнить определения.

Чему равен синус: синус угла равен отношению противоположного катета к гипотенузе.

Чему равен косинус: косинус угла равен отношению прилежащего катета к гипотенузе.

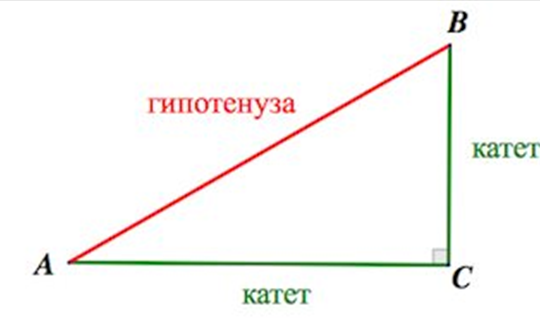
Если у нас есть треугольник \(ABC\), рисунок выше, для которого \(С\)- прямой угол, то сторонами \(BC\) и \(AC\) будут катеты, а сторона \(AB\) - гипотенуза. Следовательно, по определению, синус угла \(ABC\) равен отношению катета \(АС\) к гипотенузе: синус угла \(ABC=\frac{AC}{AB}\) и синус угла \(BAC=\frac{BC}{AB}\).

косинус угла \(ABC=\frac{BC}{AB}\) и косинус угла \(BAC=\frac{AC}{AB}\).

Чаще всего известно лишь часть данных, например катет и угол, нужно выразить неизвестную величину. Подумайте, как это сделать.

Пример 1. Вычислим синус по двум катетам.

Берем тот же треугольник \(ACB\) с прямым углом \(С\) в котором мы знаем катеты: \(BC = 3\), \(AC = 4\). Для вычисления синуса угла с необходимо разделить катет на гипотенузу: \(sin ∠BAC = \frac{BC} { AB}\).

Гипотенузу вычислим из теоремы Пифагора: \(AC^2+BC^2=AB^2\) \(9+16=25\) \(AB=5\) откуда синус равен:

\(sin ∠ BAC = \frac{3}{5}\)

Пример 2. Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).

Самое главное помнить, что сумма всех углов в треугольнике равна 180 °. Найдем угол \(ABC\):

\(180\)° \(-30\)° \(-90\)°\(=60\)°.

\(sin\) \(60\)° возьмем из табличного значения: \(\frac{ \sqrt{3}} { 2}\)

Табличные значения \(sin\) и \(cos\):

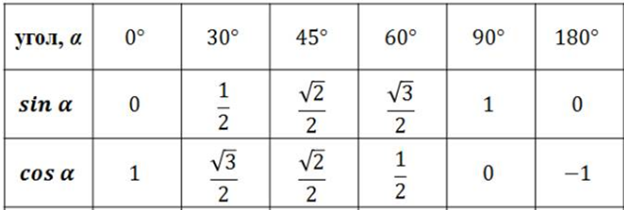
Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат \((y)\) линия синуса, ось абсцисс \((x)\) – линия косинуса. Если вы забыли значения синуса и косинуса \(90\) и \(180\) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит \(x\), на втором \(y\) \((x,y)\);

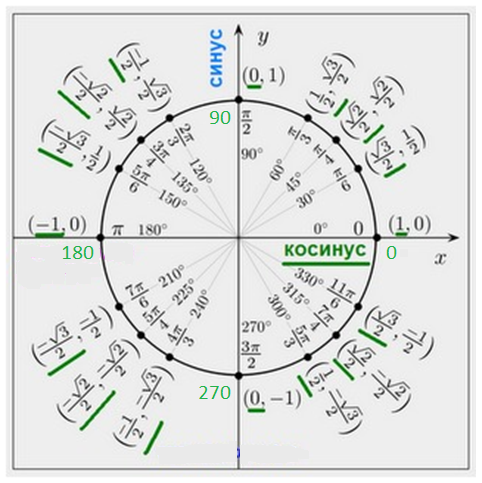
Теорема синусов:

Теорема косинусов:

Часто задаваемые вопросы:

✅ Каковы значения синуса и косинуса для угла в 0 градусов?

↪ Для угла в 0 градусов синус равен 0, а косинус равен 1.

✅ Можно ли определить синус и косинус углов, не являющихся острыми?

↪ Да, синус и косинус могут быть определены для любого угла, используя единичный круг. Значения этих функций для углов, превышающих 90 градусов, будут зависеть от четверти, в которой находится угол.

Предыдущая статья