Округление десятичных дробей

Округление десятичных дробей изучается в 5 классе. Оно нужно для удобства восприятия чисел, когда точность до определенного знака не является критически важной. Например, при измерениях в физике и инженерии точность измерения может быть ограничена прибором, и в этом случае округление чисел может быть необходимо для представления результатов измерений в более удобном и понятном виде.

Также округление может быть полезно для сокращения чисел, чтобы они занимали меньше места при хранении или передаче данных. Например, при работе с финансовыми данными, округление может быть полезно для упрощения вычислений и представления сумм в более компактном виде.

В целом, округление десятичных дробей является важным инструментом математики и естественных наук для представления результатов вычислений и измерений в более удобном и понятном виде.

Правила округления десятичных дробей следующие:

1. Если цифра после знака округления меньше 5, то число округляется до ближайшего меньшего целого числа. Например, 2.3 округляется до 2, а 4.4 округляется до 4.

2. Если цифра после знака округления равна 5, то число округляется до ближайшего четного целого числа. Например, 2.5 округляется до 2, а 3.5 округляется до 4.

3. Если цифра после знака округления больше 5, то число округляется до ближайшего большего целого числа. Например, 6.7 округляется до 7, а 9.9 округляется до 10.

4. Если цифра после знака округления равна 0, то число не изменяется. Например, 7.0 остается 7, а 12.0 остается 12.

При округлении следует учитывать количество знаков после запятой, указанное в условии задачи, либо определенное в соответствующих правилах. Также в некоторых случаях может быть указано требуемое число значащих цифр, которое также следует учитывать при округлении.

Например, вы делаете домашнюю работу и там надо ответ округлить до десятых, сотых или тысячных. И тут вы начинаете сомневаться и искать нужную для вас информацию, чтобы дать корректный ответ. В этой статье мы научим тебя правильно и просто округлять десятичные числа.

 

Округлить до ближайшей тысячной или до третьего десятичного знака число \(12,9859\). Цифры после запятой представляют собой десятые, сотые, тысячные и десятитысячные.  Нам надо найти цифру в тысячной части, остальное отбрасываем. Как вы уже догадались - это цифра \(5\), но нам важно знать какая цифра стоит после нее.

Если больше или равно \(5\), то есть \(-5,6,7,8,9\) , нам необходимо прибавить один к цифре, Результат округления - \(12,986\).

---

Задача 1. Округлите число до сотых \(13,784.\)

Решение.

Найдем цифру после запятой, которая указывает на сотые:

Далее смотрим на следующую цифру:

Так как \(4<5\), значение \(8\) не меняет своего значения. Итого получаем:

Ответ: \(13,78.\)

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

 

 

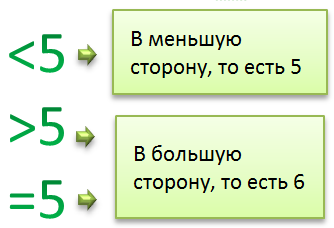
Часто задаваемые вопросы