Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость). Формула Ньютона-Лейбница

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы Абитурентам Математика Подготовка к ЕГЭ Русский язык ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ Полезное Досуг Физика

#Математика #Подготовка к ЕГЭ #ЕГЭ по математике

Обновлено: 16 апр 2024

Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость). Формула Ньютона-Лейбница

Пусть ƒ интегрируема на [a,b]. Тогда на [a,b] определена функция

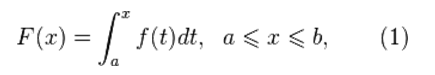
называемая интегралом с переменным верхним пределом.

Теорема 1. Пусть ƒ интегрируема на [a,b]. Тогда функция F непрерывна на [a,b].

.

Доказательство. Пусть

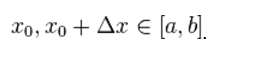
Тогда

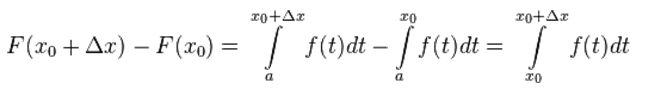
Функция ƒ ограничена на [a,b] (поскольку она интегрируема), так что при некотором M

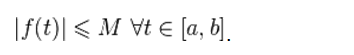
Следовательно

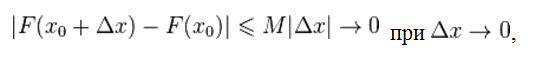
что и требовалось показать.

Теорема 2. Пусть функция ƒ интегрируема на [a,b] и непрерывна в точке

Тогда функция F(x) имеет производную в точке x0 и

Предыдущая статья

Следующая статья

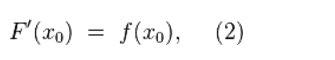
Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Площадь цилиндра

Обновлено: 24 июл 2024

Объем прямоугольной пирамиды

Обновлено: 30 авг 2024

Основные формулы производной

Обновлено: 02 окт 2024

Как найти делимое?

Обновлено: 01 мар 2025

Признак делимости на 13

Обновлено: 17 июн 2024

Как решать уравнения смешанного типа?

Обновлено: 03 авг 2024

ЕГЭ по математике, профильный уровень. Показательные уравнения

Обновлено: 06 июл 2024

Задачи с логарифмическими уравнениями и неравенствами

Обновлено: 08 фев 2025