Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Радианная мера угла
Для его измерения рассмотрим единичную окружность, где вершина угла совпадает с его центром. Затем нарисуем дугу, равную радиусу окружности и соединим концы дуги с центром.
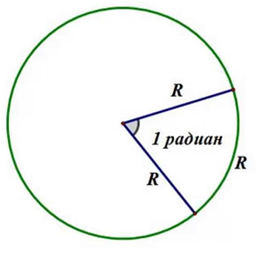
Это и есть один радиан, один градус равен \(\frac{π}{180}\) радиан и \(1\) радиан равен \(\frac{180}{π}\) градусов.
Вся окружность равна \(2π\).

Определение радиана:

Краткая история радиана
Слово "радиан" было придумано Томасом Муиром или Джеймсом Томпсоном около 1870 года, математики измеряли углы таким образом в течение длительного времени. Например, Леонард Эйлер (1707-1783) в своих исследованиях в алгебре измерял углы по длине дуги, отрезанной в единичной окружности. Это ему было необходимо для того, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции косинусов с экспоненциальной функцией.
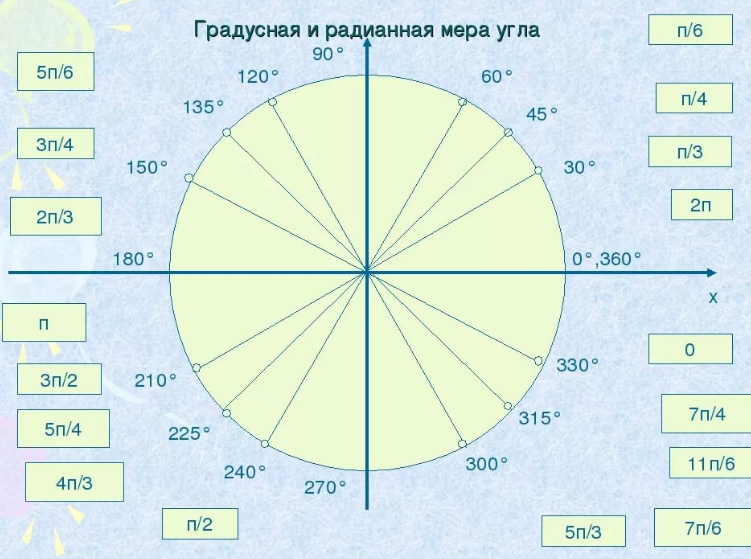
Найдите градусную меру углов, если его радианная мера равна: \(\frac{π}{2};\frac{π}{4};\frac{π}{8};\frac{5π}{6};\)
Решение.
- \(\frac{π}{2}*\frac{180}{π}=\)\(90°\)
- \(\frac{π}{4}*\frac{180}{π}=\)\(45°\)
- \(\frac{π}{8}*\frac{180}{π}=\)\(22,5°\)
- \(\frac{5π}{6}*\frac{180}{π}=\)\(150°\)
Таблица градусов в радианах

Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ЕГЭ по математике профильный уровень
Подготовка к ЕГЭ по математике профильный уровень -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Подготовка к олимпиадам по химии
Подготовка к олимпиадам по химии -
 Репетитор для подготовки к ЕГЭ по физике
Репетитор для подготовки к ЕГЭ по физике -
 Репетитор по грамматике русского языка
Репетитор по грамматике русского языка -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн -
 Репетитор по литературе ОГЭ
Репетитор по литературе ОГЭ -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

