Тригонометрическая единичная окружность, функция синуса, косинуса, тангенса и котангенса

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

26 авг 2024

Тригонометрическая единичная окружность, функция синуса, косинуса, тангенса и котангенса

Возьмем ось \(x\) и ось \(y\) , и пусть \(0\)-начало координат. Круг с центром в точке \(0\) и радиусом \(1\) — это и есть тригонометрическая окружность или единичная окружность.

Единичная окружность

Если \(P\)- точка на окружности, а \(A\)-угол между отрезком \(PO\) и \(x\), то:

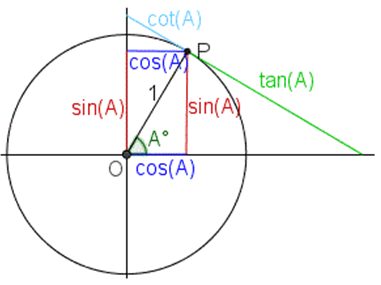
\(x\)-координата \(P\) называется косинусом \(A\). мы пишем \(cos (A)\) или \(cos A\);
\(y\)-координата \(P\) называется синусом \(A\). Мы пишем \(sin (A)\) или \(sin A\);

число \(\frac{sin (A)} { cos (A)}\) называется касательной \(A\) , мы пишем \(tg (A)\) ;

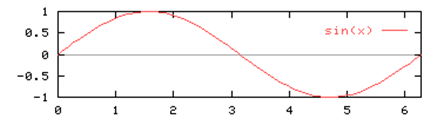
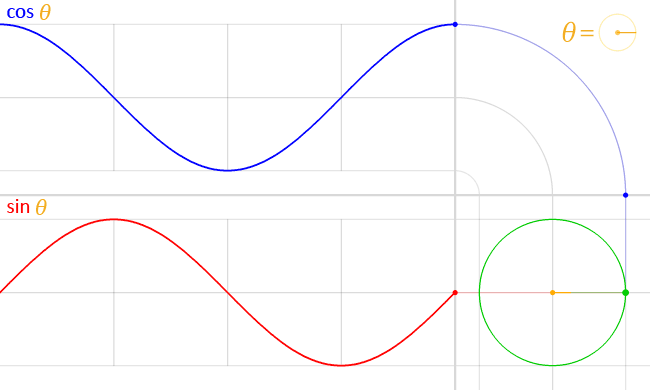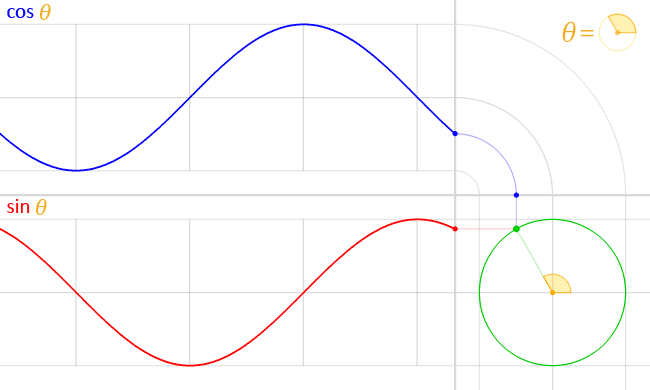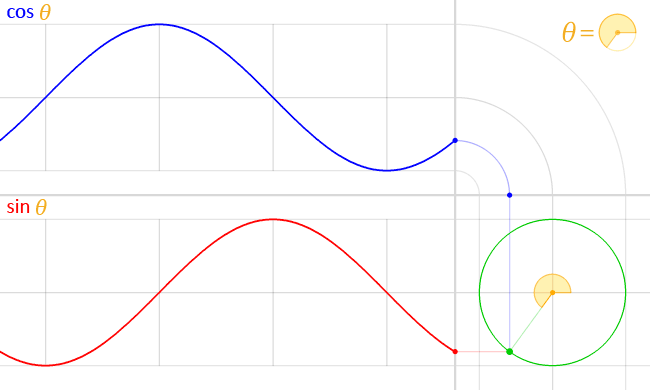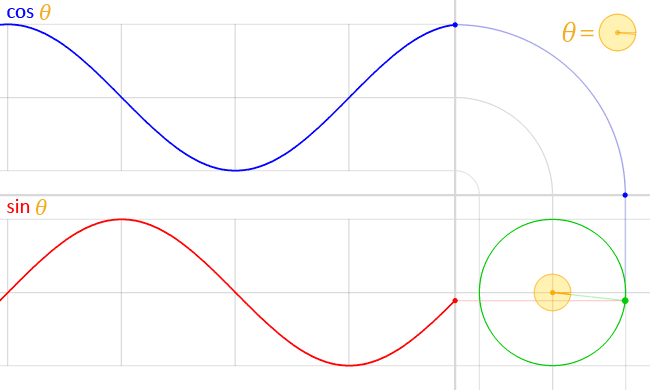
Функция синуса
\(sin: R - > [-1;1]\)

Все тригонометрические функции являются периодическими c периодом \( 2π.\)
Диапазон функции равен \([-1,1]\).

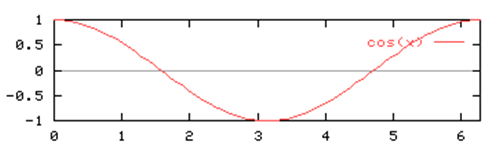
Функция косинуса
\(cos: R - > [-1;1]\)

Период \(2π\).
Диапазон функции также равен \( [-1,1]\) .

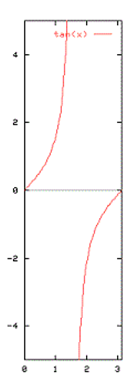
Функция тангенса
\(tan: R - > R\)

Период диапазона \(π\) функции \(R\) не определен при \( x = \frac{π}{2} + kn, k=0,1,2,...\)
График функции тангенса на интервале \(0 - π\)

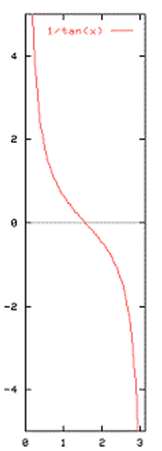
Функция котангенс
\(ctg: R - > R\)

Диапазон функции \(R\). период \(π\) и что функция не определена при \( x = kn, k=0,1,2,...\)

Часто задаваемые вопросы:

✅ Что такое тригонометрическая единичная окружность?

↪ Тригонометрическая единичная окружность - это окружность радиусом 1, центр которой находится в начале координат. Она используется для изучения связей между углами и тригонометрическими функциями.

✅ Как определить значения синуса и косинуса угла на единичной окружности?

↪ Для угла θ, синус равен y-координате точки на окружности, где луч с углом θ пересекает окружность. Косинус равен x-координате той же точки.

✅ Как связаны тригонометрические функции на единичной окружности?

↪ На единичной окружности выполняется тождество Пифагора: sin²(θ) + cos²(θ) = 1. Это означает, что квадрат синуса угла плюс квадрат косинуса угла всегда равен 1.

Предыдущая статья