Декартова прямоугольная система координат, координаты точек

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

20 авг 2024

Декартова прямоугольная система координат, координаты точек

Прямоугольная система координат или декартова система координат представляет собой пару перпендикулярных линий координат, называемых осями координат, которые расположены так, что пересекаются в начале координат.

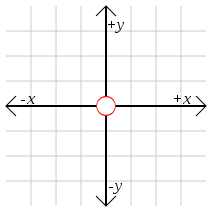
Маркировка осей буквами \(x\) и \(y\) является общепринятым соглашением, но могут использоваться также любые буквы. Если для обозначения осей координат используются буквы \(x\) и \(y\), то результирующая плоскость называется плоскостью \(xy\).

Упорядоченная пара

Под упорядоченной парой вещественных чисел мы понимаем два вещественных числа в заданном порядке. Каждая точка например \(C\) в координатной плоскости может быть связана с уникальной упорядоченной парой вещественных чисел путем рисования двух линий через \(C\), одна перпендикулярна оси x, а другая - оси Y.

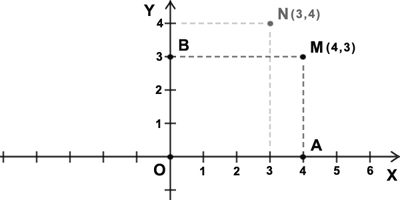
Например, возьмем две точки с координатами \((x, y)\) \(М(4,3)\) и \(N(3;4)\).

Построить точку \(M(x, y)\) означает найти точку с координатами \((x, y) \) в координатной плоскости.

Определение графика

График уравнения по двум переменным \(x\) и \(y\) представляет собой множество точек в плоскости \(xy\), координаты которых являются членами множества решений этого уравнения.

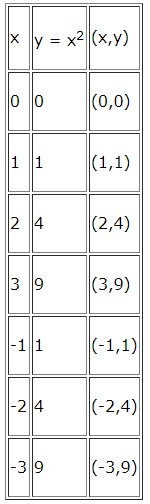
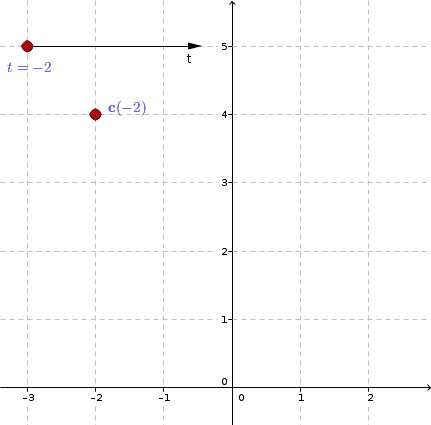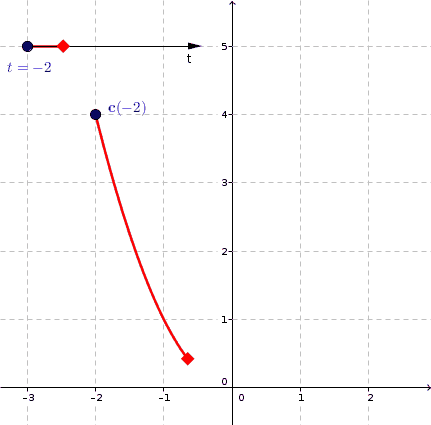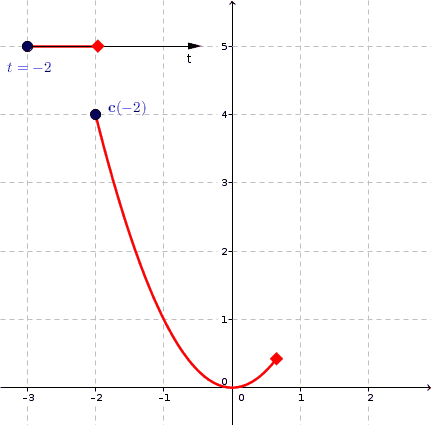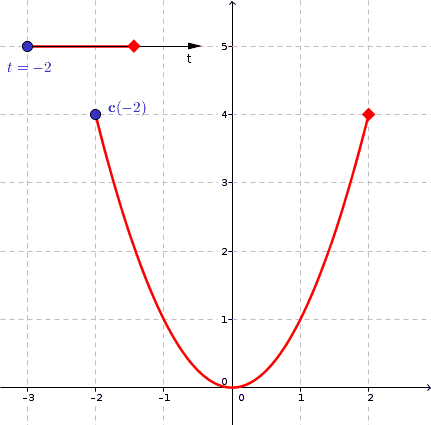
Пример: нарисуем график \(y = x^2\)

Построим точки и нарисуем график параболы \(y=x^2\) по точкам, учитывая, что \(x\) является независимой переменной, а \(y\)-зависимой переменной. Выберем некоторые значения для \(x\), а затем определим соответствующие значения \(y\).

Часто задаваемые вопросы:

✅ Каким образом задаются координаты точек на плоскости?

↪ Каждая точка на плоскости задается уникальной парой чисел (X, Y), где X - горизонтальная координата, а Y - вертикальная координата.

✅ Как называются четверти плоскости в Декартовой системе координат?

↪ Четверти плоскости делятся на I, II, III и IV квадранты, начиная с положительного направления осей и против часовой стрелки.

✅ Для чего используются координаты точек в математике и других областях?

↪ Координаты точек используются для решения геометрических задач, анализа данных, построения графиков, моделирования в физике, инженерии, компьютерной графике и многих других областях.

Предыдущая статья