Свойства параллелограмма и диагоналей параллелограмма

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

24 июн 2024

Свойства параллелограмма и диагоналей параллелограмма

Параллелограмм - это особая фигура в геометрии, которая имеет некоторые интересные свойства. Давайте рассмотрим основные свойства диагоналей параллелограмма.

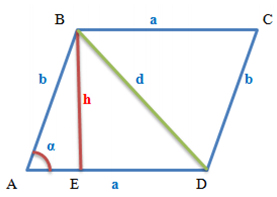
Противоположные углы параллелограмма равны.
Высота перпендикулярно основанию параллелограмма.
Cумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: \(d_1^2+d_2^2=2(a^2+b^2)\);
Диагонали в параллелограмме пересекаются в точке: \(AO = OC, BO = OD\)
Сумма углов четырехугольника прилегающих к любой стороне равна \(180°\).
Сумма квадратов диагоналей равна сумме квадратов сторон в параллелограмме: \(d^2_1+d_2^2=2a^2+2b^2.\)
Биссектрисы противоположных углов параллелограмма всегда параллельны.
Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом \(90°\).
Сторону параллелограмма можно найти по диагонали и углу между ними:

\(a= \sqrt{d_1^2 + d^2_2 - 2d_1d_2cosa } \)

Сторону параллелограмма можно найти по диагоналям и другой стороне:

\(a = { \sqrt{2d_1^2+ 2d_1^2 - 4b_2^2 } \over 2} \)

\(b = { \sqrt{2d_1^2+ 2d_1^2 - 4a_2^2 } \over 2} \)

Часто задаваемые вопросы:

✅ Какие свойства имеет параллелограмм?

↪ 1) Противоположные стороны параллелограмма параллельны и имеют одинаковую длину. 2) Противоположные углы параллелограмма равны. 3) Соседние углы параллелограмма дополнительны.

✅ Что происходит с диагоналями параллелограмма?

↪ Диагонали параллелограмма делят его на два равных треугольника. Диагонали параллелограмма пересекаются в точке, которая делит их пополам.

✅ Какие задачи можно решать с использованием свойств параллелограмма?

↪ С использованием свойств параллелограмма можно решать задачи, связанные с вычислением площади, углов и других параметров фигуры. Например, можно вычислять площадь параллелограмма, находить значения углов, определять длины сторон и проверять, является ли данная фигура параллелограммом.

Предыдущая статья