Касательная к окружности. Точка касания окружности

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы Абитурентам Математика Подготовка к ЕГЭ Русский язык ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ Полезное Досуг Физика

#Математика #Подготовка к ЕГЭ #ЕГЭ по математике #ОГЭ по математике #Подготовка к ОГЭ

Обновлено: 18 апр 2024

Касательная к окружности. Точка касания окружности

Линии могут пересекать окружность в двух точках, они называются секущими, а некоторые линии могут вообще не пересекать окружность. Линии, которые пересекают окружность в одной точке называются касательными линиями или просто касательными к окружности из заданной точки. Из одной точки можно провести только две касательные:

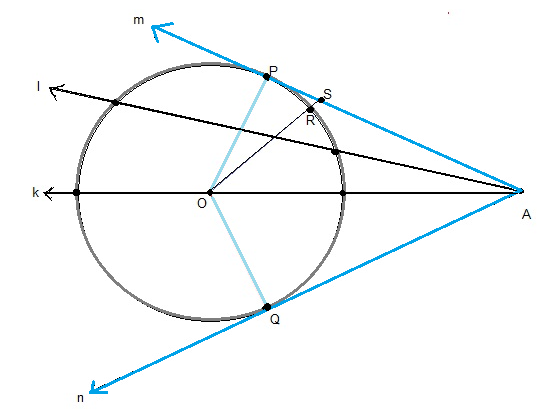
Рисунок выше показывает окружность с центром в точке \(O\) и точкой \(A\) вне окружности. Линии \(k, l, m \) и \(n\) выходят из точки \(A\) и пересекают окружность.

Линии \(k\) и \(l\) пересекают окружность в двух точках, и, следовательно, эти линии не являются секущими к окружности.
Линии \(m\) и \(n\) касаются окружности только в одной точке, и поэтому каждая из этих линий называется касательной к окружности из точки A.
Любая линия, проведенная над касательной \(m\) или под касательной \(n\) не будет пересекать окружность.

Может существовать бесконечное количество секущих к окружности из одной точки, но может существовать только две касательные к окружности из одной и той же точки.

Точка касания - это точка соприкосновения касательной линии с окружностью . На рисунке выше это точки \(Q \) и \(P\).

Выведем несколько важных понятий на эту тему. Рассмотрим рисунок выше: \(OP-\) это радиус, который соединяет центр окружности и точку касания \(P\). Возьмем другую точку \(S\) где-нибудь на касательной линии и свяжем ее также с центром окружности. Длина \(OS\) больше \(RS\), \(OS\) равна \(OP + OS\), так как \(OR\) и \(OS\) являются радиусами одного круга. Следовательно, расстояние \(OP\) меньше, чем расстояние \(OS\), за исключением случаев, когда они совпадают. Согласно геометрическим данным радиус должен быть перпендикулярен касательной линии в точке касания.

Выводы:

кратчайший путь к касательной от центра окружности - это радиус окружности в точке касания;
радиус окружности, всегда находится под прямым углом к касательной в точке касания.

Далее рассмотрим треугольники \(OPA\) и \(OQA\). \(OA\) является общей стороной, разделяемой обоими треугольниками, \(OP\) и \(OQ-\) радиусы и они равны, \(AP\) и \(AQ\) также равны между собой. Следовательно, треугольники \(OPA\) и \(OQA\) равны между собой.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Касательная к окружности. Точка касания окружности

Касательная к окружности. Точка касания окружности

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи