ЕГЭ по математике, профильный уровень. Неравенства

Условие:

Решите неравенство

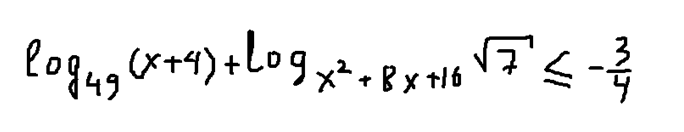
Решение

В этом неравенстве видим, что основания логарифмов разные. Однако второе основание можно преобразовать по формуле сокращенного умножения и получить выражение, идентичное выражению первого логарифма. Этим обстоятельством мы воспользуемся, чтобы сделать преобразования.

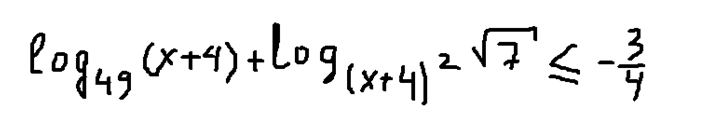
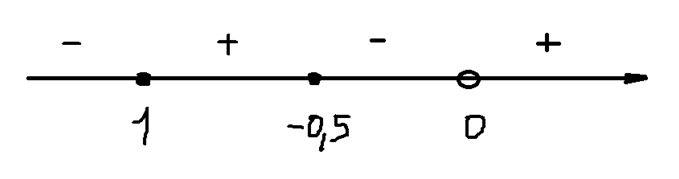
Далее найдем ОДЗ этого выражения:

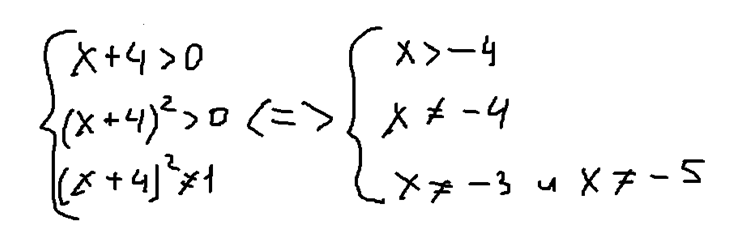
Отметим точки на числовой оси и найдем ОДЗ:

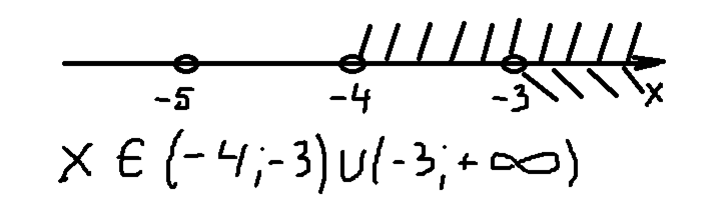
Продолжим преобразования неравенства, чтобы еще более упростить его. Представим «49 = 7²», а радикал заменим степенью:

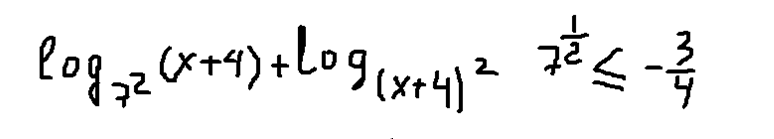
Используя свойства логарифмов, запишем:

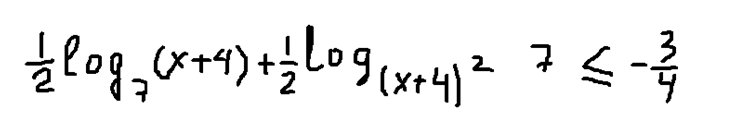
Далее умножим обе части неравенства на «2»:

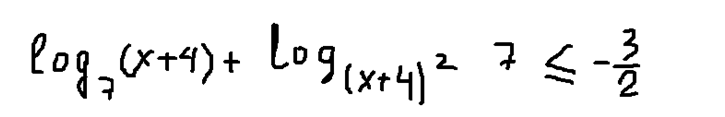
Чтобы привести логарифмы к одному основанию, также воспользуемся их свойствами и разделим второй логарифм на «1»:

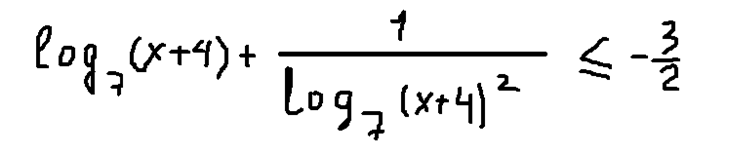
Далее преобразуем:

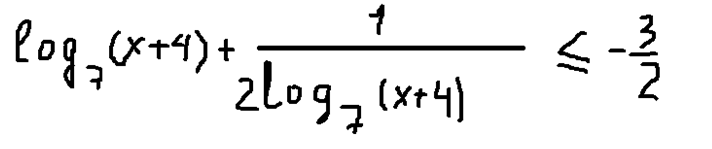
А теперь сделаем замену переменных:

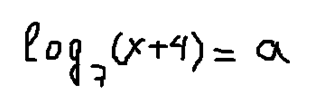
Такая замена переменных позволит нам записать:

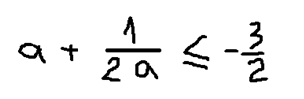
Умножим обе части уравнения на «2»:

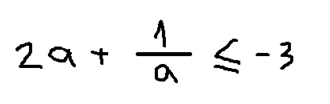
Перенесем «-3» в левую часть:

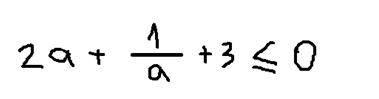
Далее найдем общий знаменатель:

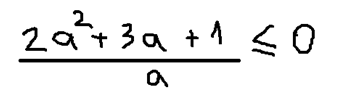
Решим числитель как квадратное уравнение, найдем корни, учитывая, что a ≠ 0

Получаем два корня:

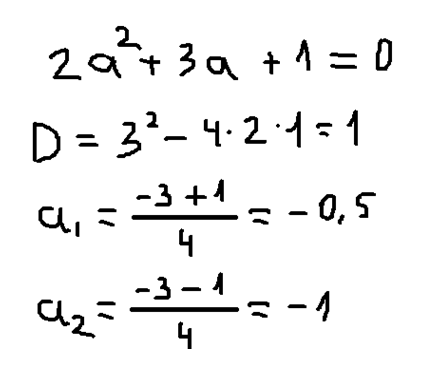
Зная корни, разложим числитель на множители:

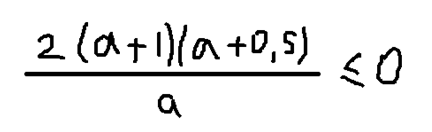
Найдем на числовой оси знаки на промежутках:

Продолжим, сделаем обратную замену переменных и найдем корни:

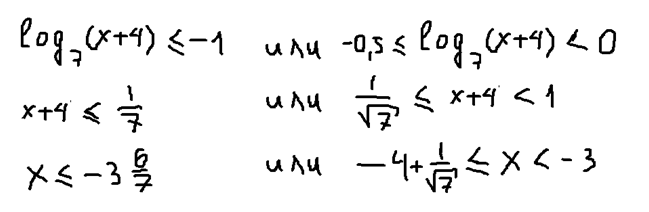
Отметим эти точки на числовой оси и обозначим интервалы, являющиеся решением:

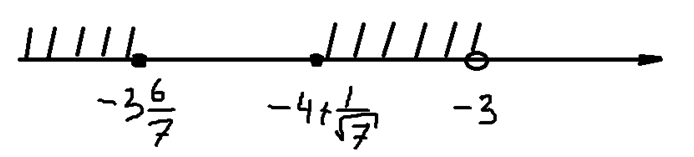
Обязательно совместим этот результат с выводами по определению ОДЗ, полученные вначале, также отметив их на числовой оси:

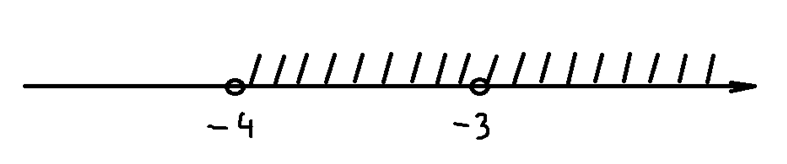
Совместим полученные интервалы и запишем окончательный ответ:

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Правила вычитания векторов

Обновлено: 04 июн 2024

Пирамида и ее свойства

Обновлено: 07 окт 2024

МИФИ (Экономическая Безопасность): Проходной балл, учебный план

Обновлено: 16 июл 2024

ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 3)

Обновлено: 22 авг 2024

ОГЭ по математике, базовый уровень. Числа и вычисления

Обновлено: 15 дек 2024

ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений

Обновлено: 08 янв 2025

Как решать задание №21 из ОГЭ по математике

Обновлено: 17 ноя 2024

Задачи с прикладным содержанием (вариант 3)

Обновлено: 11 дек 2024