Движение вдогонку

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

23 сен 2024

Движение вдогонку

Задачи, в которых двигаются вдогонку из разных пунктов, решают по определенному правилу.

Два объекта могут сближаться или удаляться в зависимости от их скоростей:

Если скорость объекта впереди больше, то они удаляются.

Если скорость объекта впереди меньше, то они сближаются

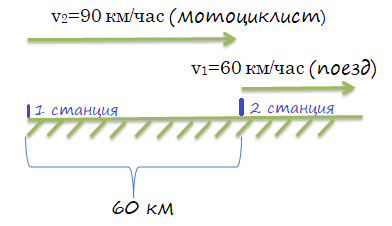
Задача 1. \(S\) между двумя станциями \(60\) км. Одновременно в одном и том же направлении выехали поезд и мотоциклист, так что поезд едет впереди. Через сколько часов мотоциклист догонит поезд, если его скорость равна \(90\) км/ч, а скорость поезда — \(60\) км/ч?

Решение:

1) \(90-60=30\) км/час скорость сближения.

2)\(60:30 =2\) часа понадобится мотоциклисту, чтобы догнать поезд.

Ответ: \(2\) часа.

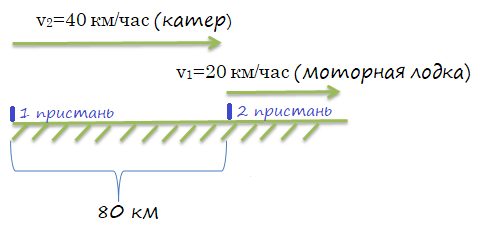
Задача 2. \(S\) между двумя пристанями равно \(80\) км. Одновременно из этих пристаней в одном направлении выплывают катер и моторная лодка, так что моторная лодка плывет впереди. Скорость моторной лодки равна \(20\) км/ч, скорость катера — \(40\) км/ч. На каком расстоянии от своей пристани катер догонит моторную лодку?

Решение:

1)\(40-20=20\) км/час скорость сближения.

2)\(80:20= 4\) через такое время катер догонит моторную лодку.

3)\(4*40=160 \) км такой путь пройдет катер, прежде чем догонит моторную лодку.

Ответ: \(160 \) км.

Часто задаваемые вопросы:

✅ Какие факторы могут влиять на движение вдогонку?

↪ Факторы, влияющие на движение вдогонку, включают скорость обоих тел, расстояние между ними и изменения в их скорости.

✅ Как изменяется скорость и расстояние между телами в движении вдогонку?

↪ Если оба тела движутся с постоянной скоростью и в одном направлении, то расстояние между ними остается постоянным, а скорость второго тела равна скорости первого.

Предыдущая статья