Учимся решать задачи по планиметрии

Условие:
 
В остроугольном треугольнике ABC провели высоту BH, из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
 
Решение
 
 
 
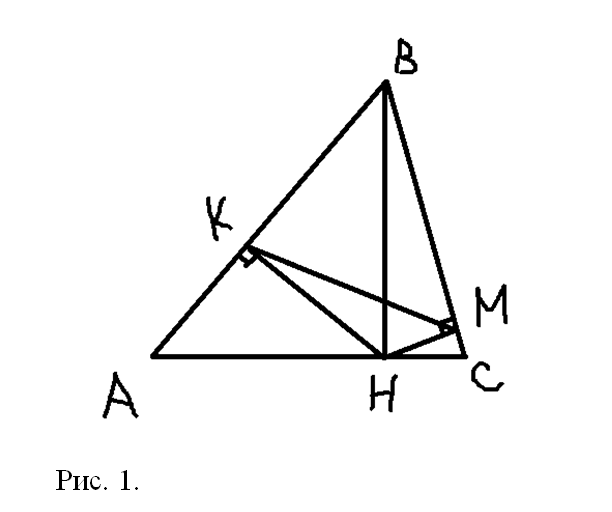
а) Изобразим заданный треугольник, обозначим вершины и точки (рис. 1).
 
Очевидно, что углы BAC и KHB равны как углы с взаимно перпендикулярными сторонами.
 
Теперь рассмотрим четырёхугольник BKHM. Мы видим, что в нем ∠BKH + ∠BMH = 90° + 90° = 180°
 
Отсюда, по свойству четырехугольников, вписанных в окружность, четырёхугольник BKHM вписан в окружность. Это значит, что углы KHB и KMB являются вписанными в окружность, и опираются на одну и ту же дугу. Из чего следует, что они равны. Таким образом, ∠BAC = ∠KHB = ∠KMB. Треугольники ABC и MBK имеют общий угол B, а ∠BAC = ∠KMB, значит, эти треугольники подобны по двум углам.
 
б) Из прямоугольного треугольника BKH, используя определение синуса угла, находим, что:
 
  
 
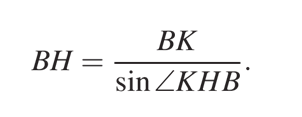
Для треугольника ABC, с учетом доказанного ранее, будет справедливо равенство:
 
 
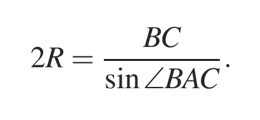
Зная, что ∠KHB = ∠BAC, получим: \({BC\over BK}={2R\over BH}\)
 
  
Стороны BC и BK являются сходственными в подобных треугольниках ABC и MBK, их коэффициент подобия равен:
 
 \(k={BC\over BK}={2R\over BH}=4\)
 
Найдём отношение площади треугольника MBK к площади четырёхугольника AKMC:
 
 
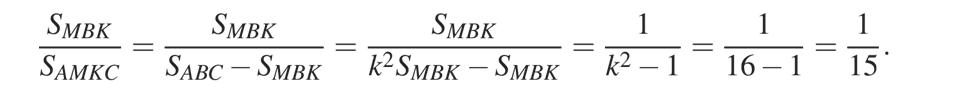
Ответ: \(1 \over 15\)
 
Автор - Андрей Найденов
 
 
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Виктория Дмитриевна Доненко
Репетитор по математике
Стаж (лет)
11
Образование:
Украинский химико-технологический университет
Проведенных занятий:
0
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии. Химия - непростая наука, зато очень интересная и для некоторых даже загадочная. Химия - царица наук! Большая половина предметов, окружающих нас - это химия. Моя задача: открыть логичность и последовательность химии на своих занятиях.
Зоя Юрьевна Духненко
Репетитор по математике
Стаж (лет)
30
Образование:
Душанбинский государственный педагогический институт им. Т. Г. Шевченко
Проведенных занятий:
3
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-8 классов. Подготовка к ОГЭ. Я люблю математику и очень стараюсь привить эту любовь детям. Ведь без математики наша жизнь была бы скучной и однообразной, мы много бы не узнали об окружающем нас мире. К каждому ребенку нахожу индивидуальный подход. Объясняю доступно, легко и просто.
Жанна Александровна Бояркина
Репетитор по математике
Стаж (лет)
28
Образование:
Благовещенский государственный педагогический институт
Проведенных занятий:
28
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное - понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда. Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах. На уроках придерживаюсь трех единств: наглядно, понятно, просто.

Математика 11 класс
  • - Индивидуальные занятия
  • - В любое удобное для вас время
  • - Бесплатное вводное занятие
от 590 ₽ Хочу бесплатный урок

Курсы ОГЭ
  • - Индивидуальные занятия
  • - В любое удобное для вас время
  • - Бесплатное вводное занятие
от 590 ₽ Хочу бесплатный урок

Репетитор по математике (1 класс)
  • - Индивидуальные занятия
  • - В любое удобное для вас время
  • - Бесплатное вводное занятие
от 590 ₽ Хочу бесплатный урок
Похожие статьи