ЕГЭ по математике, профильный уровень. Показательные уравнения
Как научиться решать уравнения? На самом деле все не так страшно, как кажется многим школьникам. Прежде всего, нужно знать алгоритмы решения типовых заданий. Именно с этой целью мы размещаем в блоге подробные решения реальных заданий из ЕГЭ прошлых лет.
Условие:
а) Решите уравнение ![]()
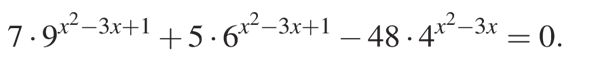
б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
Решение:
а) Обратите внимание, что показатели степени у первого и второго слагаемых совпадают, а показатель степени у третьего слагаемого почти совпадает с предыдущими. Преобразуем уравнение так, чтобы и третий показатель степени стал трехчленом, как первый и второй:
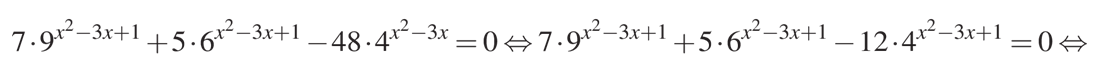
Теперь займемся преобразованием оснований степени так, чтобы было удобно найти корни. Для этого приведем это уравнение к квадратному, оставив третье слагаемое как свободный член:
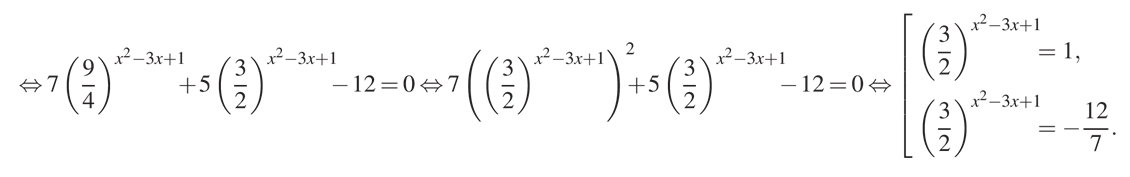
Итак, мы получили два уравнения. Мы видим, что у второго уравнения решений нет, так как правая часть с минусом. Это упрощает дальнейшее решение.
Мы преобразуем первое уравнение к виду, используя стандартные шаги при решении показательного уравнения:
\(x^2-3x+1=0\)
Откуда, после нахождения дискриминанта, получим два корня:
\({x}={{3±\sqrt5}\over2}\)
б) Для ответа на второй вопрос оценим \(\sqrt5\) целыми числами:
\(2<\sqrt5<3\)
Тогда получим, что:
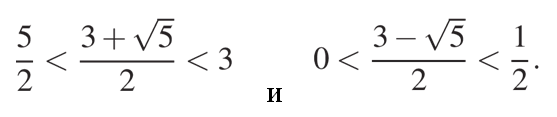
Отсюда видно, что отрезку [-1;2] принадлежит только корень: \({x}={{3-\sqrt5}\over2}\)
Ответ: а) \({{3±\sqrt5}\over2}\) б) \({{3-\sqrt5}\over2}\)
Автор - Андрей Найденов
Наши преподаватели
Репетитор по математике
Стаж (лет)
21
Образование:
Рязанский государственный педагогический университет имени С. А. Есенина
Проведенных занятий:
772
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
13
Образование:
Минский государственный лингвистический университет
Проведенных занятий:
33
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
6
Образование:
Гродненский государственный университет имени Янки Купалы
Проведенных занятий:
40
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по алгебре
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор по химии для подготовки к ОГЭ
- Подготовка к олимпиадам по химии
- Репетитор для подготовки к ОГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ОГЭ по истории
- Репетитор по информатике для подготовки к ОГЭ
Похожие статьи
- Основные формулы: треугольник, параллелограмм и четырехугольник
- Вычисление средней скорости
- МФТИ (Системный Анализ и Управление): отзывы, проходной балл, вступительные испытания
- ЕГЭ по математике, профильный уровень. Уравнения
- Интересные факты из области математики
- Вместе — все по плечу: фильмы и мультики о братьях и сестрах
- Осенняя фотосессия: идеи для креативных снимков
- День матери: что подарить самому близкому человеку?
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так