Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Задачи на вклад в банк
Условие:
За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом \({11}{1\over9}\)% и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на \({104}{1\over6}\)%. Определите срок хранения вклада.
Решение:
Итак, из условия задачи нам известно:
- Проценты на вклад начислялись ежемесячно.
- Каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.
- Процентная ставка в течение срока хранения вклада изменялась четыре раза
- Изменение процентной ставки происходило в том порядке, который отражен в условии задачи.
На основании условия задачи, сделаем необходимые последовательные шаги:
1)Если первоначальная сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась, например, k месяцев, то вклад ежемесячно увеличивался в \(1+5*0,01\) раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.
2)При изменении процентной надбавки c 5% на 12% (ставка 12% продержалась, например, m месяцев) первоначальная сумма вклада за k+m месяцев увеличится в \((1+0,05)^k*(1+0,12)^m=({21\over20})^k*({28\over25})^m\) раз.
3)Предположим, что процентная ставка \({11}{1\over9}\) продержалась, например, n месяцев: \((1+{100\over9}*0,01)^n=({10\over9})^n\)
4)Предположим, что процентная ставка 12,5 продержалась, например, t месяцев: \((1+12,5*0,01)^t=({9\over8})^t\)
Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке будет равен произведению составленных выше условий и составит:
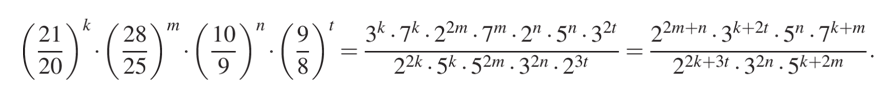
Полученное выражение отражает все изменения с процентной ставкой за весь период размещения вклада.
С другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на \({104}{1\over6}\), то есть в
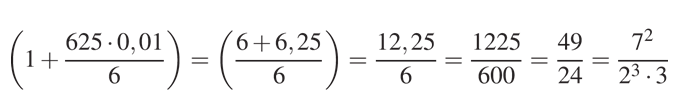 раз.
раз. Значит:
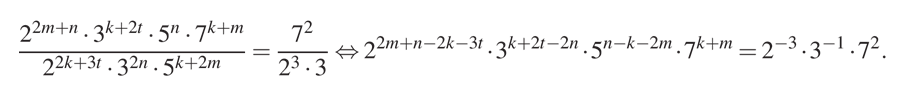
Получилось выражение, в котором имеются множители, стоящие в степени.
Вспомним основную теорему арифметики:
Каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования.
Используя эту теорему, мы можем записать:
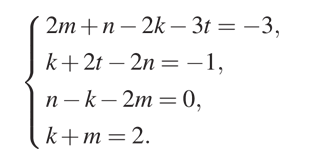
Получается система из четырех уравнений с четырьмя неизвестными. Это вполне доступный для решения вариант. Решим эту систему относительно натуральных k, m, n и t.
Из последнего уравнения системы, с учетом того, что неизвестные являются целыми положительными числами, получаем: \(k=m=1\) При этих значениях k и m система примет более простой вид:
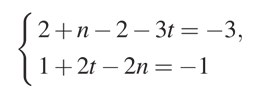
Это система из двух уравнений с двумя неизвестными. Решим её:
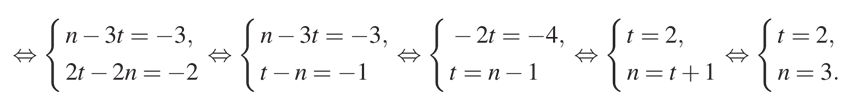
Итак, \(k+m+n+t=1+1+3+2=7\). Вклад в банке на хранении был 7 месяцев. При найденных значениях k, m, n и t выражение действительно равно нулю.
Ответ: 7.
Автор - Андрей Найденов
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор для подготовки к ОГЭ по математике
Репетитор для подготовки к ОГЭ по математике -
 Подготовка к ЕГЭ по математике профильный уровень
Подготовка к ЕГЭ по математике профильный уровень -
 Репетитор для подготовки к ЕГЭ по химии
Репетитор для подготовки к ЕГЭ по химии -
 Репетитор по английскому ОГЭ онлайн
Репетитор по английскому ОГЭ онлайн -
 Подготовка к ЕГЭ по истории
Подготовка к ЕГЭ по истории -
 Репетитор по математике впр
Репетитор по математике впр -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн -
 Репетитор по литературе ОГЭ
Репетитор по литературе ОГЭ -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

