Сложение векторов
Предметы
Специализации
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к ОГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор по грамматике английского языка
- Репетитор для подготовки к ВПР по английскому языку
- ВПР по физике
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ОГЭ
Сложение векторов с помощью правила треугольника, параллелограмма
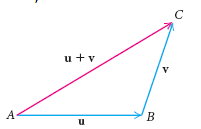
Нарисуем горизонтально вектор \(\overline{AB}\) c заданным направлением, из конца вектора \(\overline{AB}\) нарисуем вектор \(\overline{BC}\), соеденим \(А\) с \(С\). Вектор \(\overline{AC}\) называется суммой и является результирующим векторов \(\overline{AB}\) и \(\overline{BC}\):
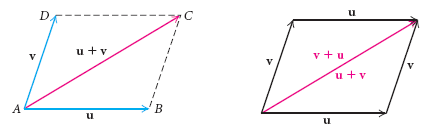
Также мы можем описать сложение векторов с помощью правила параллелограмма, где результирующим векторов \(\overline{AD}\) и \(\overline{AB}\) будет диагональ параллелограмма \(\overline{AC}\). Векторное сложение коммутативно. Как показано на рисунке справа ниже, \(\overline{u} +\overline{ v}\) и \(\overline{v} + \overline{u}\) представлены одним и тем же направленным отрезком линии \(\overline{AC}\):
Задача 1. Самолет движется со скоростью \(190\) км/ч, а ветер дует со скоростью \(48\) км / ч. угол \(OCB = 120°\) на рисунке ниже. Найти скорость самолета.
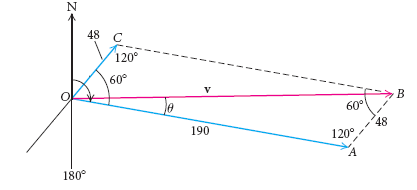
- \(∠OCB = 120°\)
- \(|v|^2 = 48^2 + 190^2 - 2*48*190*cos120° \) \(-->\) \(|v|^2 = 47,524\) \(-->\) \(|v| = 218\)
Таким образом скорость самолета \(218\) км/час.
Наши преподаватели
Репетитор по математике
Стаж (лет)
2
Образование:
Казанский государственный энергетический университет
Проведенных занятий:
63
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
20
Образование:
Пятигорский государственный педагогический институт иностранных языков
Проведенных занятий:
72
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
6
Образование:
Петрозаводский государственный университет
Проведенных занятий:
536
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Площадь поверхности треугольной пирамиды
- Основные формулы производной
- Как перевести сантиметры в дециметры
- НИУ ВШЭ (Программная инженерия): проходной балл, отзывы
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 2)
- Решаем профильный ЕГЭ. №17. Оптимизация
- Задачи на прогрессии
- Что делать, если школьник придумывает истории и жалуется родителям на преподавателя?