Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Геометрическая прогрессия
Для начала разберемся, что такое геометрическая прогрессия (ГП).
Геометрическая прогрессия – это бесконечная последовательность чисел, записанная в виде: b1, b2, ..., bn, …, где b1 - первый член, b2 - второй член, bn - «энный» член прогрессии.
Каждый член этой прогрессии, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число «q».
Число «q» называется знаменателем прогрессии.
Любой член геометрической прогрессии вычисляется по формуле:
bn = b1 q n - 1
Сумма «n» первых членов геометрической прогрессии вычисляется как:
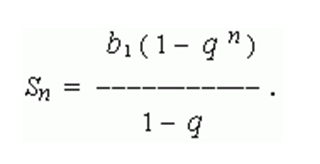
Интерес также представляет «бесконечно убывающая геометрическая прогрессия» — это геометрическая прогрессия, у которой | q | < 1 . Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии, а именно: это число «к», которому неограниченно приближается сумма «n» первых членов рассматриваемой прогрессии при неограниченном возрастании числа «n».
Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:
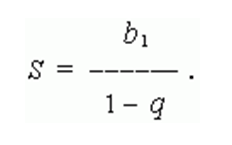
Пример геометрической прогрессии
Приведем примеры задач, где необходимо использовать эти формулы.
Пример 1
Найти девятый член (b(9)) заданной последовательности чисел: 1, 3, 9, 27, …
Решение
Данная последовательность чисел является геометрической, так как при делении каждого её члена на предыдущий получается одно и то же число «3»:
3 : 1 = 3
9 : 3 = 3
27 : 9 = 3
Следовательно, знаменателем рассматриваемой последовательности является число q = 3.
Применим формулу для нахождения суммы «n» первых членов геометрической прогрессии и найдем b(9):
bn = b1 q n - 1
b9 = 1 х 3 9 - 1 = 1 х 3 8 = 1 х 6561 = 6561
Пример 2
Найти сумму членов бесконечно убывающей геометрической прогрессии:
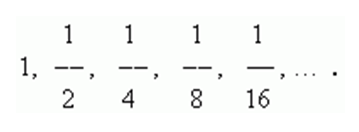
Решение
Применим формулу для вычисления суммы бесконечно убывающей геометрической прогрессии. В нашем примере b1 = 1, q = 1/2.
Тогда:
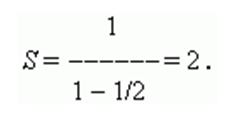
Часто задаваемые вопросы
Как определить, является ли ГП возрастающей или убывающей?
Если знаменатель (r) больше 1, то ГП является возрастающей. Если 0 < |r| < 1, то ГП убывающая.
Как найти среднее геометрическое членов ГП?
Среднее геометрическое членов ГП находится как корень из произведения двух соседних членов: √(aₙ₋₁ * aₙ).
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике -
 Подготовка к олимпиадам по химии
Подготовка к олимпиадам по химии -
 Подготовка к ОГЭ по русскому 9 класс
Подготовка к ОГЭ по русскому 9 класс -
 Репетитор по английскому ОГЭ онлайн
Репетитор по английскому ОГЭ онлайн -
 Подготовка к олимпиадам по английскому языку
Подготовка к олимпиадам по английскому языку -
 Подготовка к ВПР по русскому
Подготовка к ВПР по русскому -
 Репетитор ЕГЭ по обществознанию
Репетитор ЕГЭ по обществознанию -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Репетитор по литературе ОГЭ
Репетитор по литературе ОГЭ -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

