Ззадание №11 из ЕГЭ. Текстовые задачи

Задача №1

На кольцевой автодороге расположены четыре бензоколонки: A, B, C, D. Расстояние между A и B – 75 км, между A и C – 50 км, между C и D – 40 км, между A и D – 60 км (все расстояния измеряются по кольцевой дороге по кратчайшей дуге). Найдите расстояние между B и D (в км).

Решение

Составим схему бензоколонок (Рис.1):

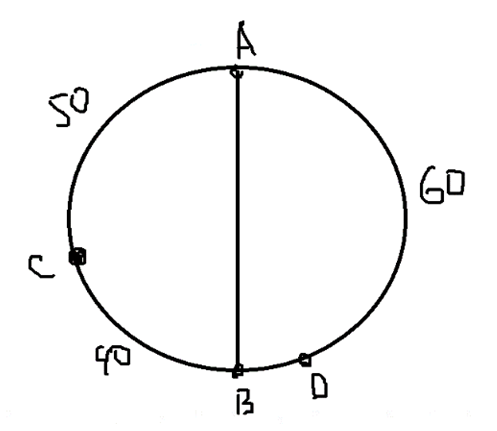
Рис.1

Расставим бензоколонки, согласно условию задачи, чтобы расстояния между ними были кратчайшими по дуге.

Начнем со второго условия:

между A и C – 50 км

между C и D – 40 км

между A и D – 60 км

Тогда мы сможем замкнуть круг и вычислить длину кольцевой дороги:

50 + 40 + 60 = 150 км

Так как расстояние между A и B – 75 км, то искомая точка будет строго по диагонали от точки А.

Тогда, исходя из схемы, получаем, что расстояние между B и D равно:

75 – 60 = 15 км

Ответ: 15 км

Задача № 2

Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.

Решение

В первый день Вася решил:

а₁ = 5 задач

в последний – «а₁₄» :

Всего надо решить:

S₁₄ = 434 задачи

По формуле для арифметической прогрессии:

можем посчитать:

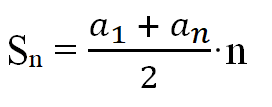
можем подсчитать:

При

а₁ = 5

n = 14

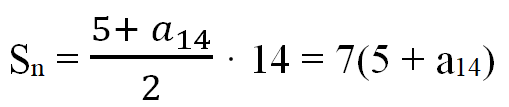
Тогда:

434 = 7(5 + a₁₄)

5 + а₁₄ = 62

а₁₄ = 57

Получаем, что Вася в последний день решил 57 задач.

Ответ: 57.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Александр Николаевич Мельничук

Репетитор по математике

Стаж (лет)

Образование:

Приднестровский государственный университет им. Т.Г. Шевченко

Проведенных занятий:

752

Форма обучения:

Дистанционно (Скайп)

Антон Евгеньевич Кукьян

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Елена Сергеевна Журова

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университет им. М. Танка

Проведенных занятий:

315

Форма обучения:

Дистанционно (Скайп)

Предметы

Специализации