ЕГЭ по математике, профильный уровень. Иррациональное уравнение

Продолжаем готовиться к экзаменам вместе с лучшими преподавателями Альфа-школы. В новой статье Андрей Алексеевич показывает подробное решение задачи из темы "Иррациональное уравнение".

Условие:

а) Решите уравнение

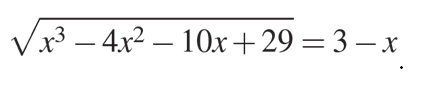б) Укажите все корни этого уравнения, принадлежащие промежутку \([-\sqrt3;\sqrt30]\).

Решение

Основным способом решения таких уравнений является возведение «в квадрат» обеих частей уравнения. Это позволяет избавиться от квадратного корня, а значит, уйти от иррациональности. Однако возведение обеих частей «в квадрат» накладывает существенное условие, которое необходимо выполнять. А именно – правая часть уравнения должна быть обязательно больше или равна нулю.

а) Начнем решать это уравнение:

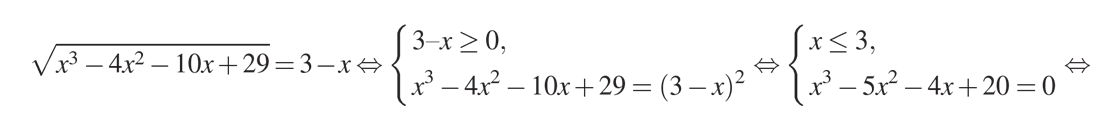
Как видите, мы учли, что правая часть исходного уравнения «3 – х» больше или равна нулю. После возведения в квадрат обеих частей мы раскрыли скобки в правой части по формуле сокращенного умножения, перенесли получившееся выражение в левую часть и привели подобные. Получилось кубическое уравнение. Сгруппируем выражение в левой части:

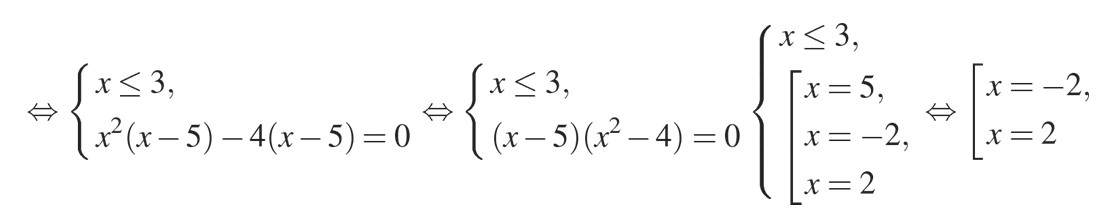
Как видите, из получившихся трех корней только два удовлетворяют условию «3 – х» больше или равна нулю.

Первая часть задания выполнена, уравнение решено.

б) Чтобы найти корни, удовлетворяющие заданному промежутку, необходимо оценить, чему будет равен «корень из трех» и «корень из 30», относительно «-2» и «2», не забывая о «минусе» перед числами. Либо оценить и сравнить между собой «квадраты» всех участвующих в оценке чисел, т.е. «квадрат 2», «квадрат корня из 3» и «квадрат корня из 30». Получаем, что:

\(-2<-\sqrt3<2<\sqrt30\)

Отсюда видно, что заданному отрезку \([-\sqrt3;\sqrt30]\) принадлежит только число 2.

Ответ: а) {-2;2}; б) 2.

Автор - Андрей Найденов

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Павел Андреевич Демин

Репетитор по математике

Стаж (лет)

Образование:

Южно-Уральский Государственный Гуманитарно Педагогичесий Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 8-11 классы. Веду подготовку к ОГЭ/ЕГЭ/ВПР Математика-царица точных наук, следовательно, она помогает в жизни выстраивать точные последовательности действий, организует, а также всегда может пригодится в быту. Работаю по принципу "пирамиды": от простого к сложному. Всегда ищу индивидуальный подход к каждому ученику, разрабатываю индивидуальные планы осваивания материала. Люблю работать как с сильными, так и слабыми учениками. Нравится разбираться в задачах вместе с учеником, наводящими вопросами выстраивать логическую цепочку решений.

Елена Сергеевна Чаплина

Репетитор по математике

Стаж (лет)

Образование:

Омский государственный педагогический институт им. А.М.Горького

Проведенных занятий:

304

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике для 5-9 классов. Подготовка к ОГЭ. Математика ум приводит в порядок. Развивает логическое мышление. Учит правильно выстраивать алгоритмы решения жизненных ситуаций и проблем. И у меня огромное желание и большой опыт работы в репетиторстве, чтобы помогать ученикам осваивать этот сложный и столь необходимый предмет. Каждый мой ученик - полноценная личность. И для работы с каждым из них я подбираю свои "ключики".

Юрий Павлович Грязнов

Репетитор по математике

Стаж (лет)

Образование:

Донецкий государственный университет

Проведенных занятий:

948

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов. Математика двигает человечество вперёд. Она помогает учёным познать окружающий мир. Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума. Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата. Самое главное в работе с детьми - настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.