Функция

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 30 янв 2024

Функция

Функции играют фундаментальную роль во всех областях математики, а также в других науках и инженерии. Более абстрактные области математики, такие, как теория множеств, рассматривают очень общие типы функций, которые не могут быть определены конкретным правилом и не регулируются какими-либо знакомыми принципами. Характерным свойством функции является то, что она связывает ровно одно значение из множества x одному значению из y.

Математическое понятие функции выражает зависимость между двумя величинами, одна из которых независимая переменная x, аргумент функции или ее "входящее значение", а другая зависимая переменная — y "выходящее значение".

Функцией, заданной на множестве \(D\), называется закон, по которому каждому значению \(x\) из множества \(D\) ставится в соответствии одно определенное значение y. Будем обозначать функцию какой-нибудь буквой, например f, а ее значение в точке x будем обозначать \(f(x)\), произносится “эф от икс”, \(y\) является функцией от \(x\) и это записывают как равенство \(y=f(x)\). Мы можем обозначать функцию и другими буквами, например \(t,r,n.\)

Областью определения функции f называется множество всех допустимых значений переменной x от функции f. Функция может быть определена только для тех значений, при которых выражение f(x) имеет смысл.

Областью значений функции f называют множество значений, которые может принимать функция f.

Задать функцию — это значит описать какую-то конкретную зависимость так, чтобы каждый мог разобраться, о чем идет речь.

Чтобы задать функцию, нужно:

записать формулу, которая задает функцию;
нарисовать график функции;
составить таблицу значений функции

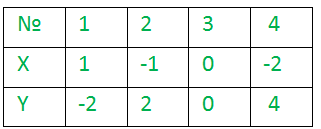
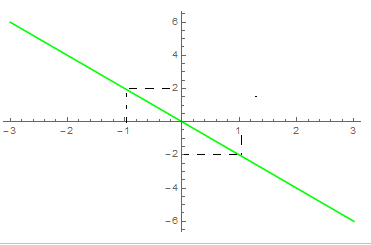
Аргумент функции — это независимая переменная, от значений которой зависят значения функции. На рисунке нарисованы таблица значений и график функции \(y=-2x:\)

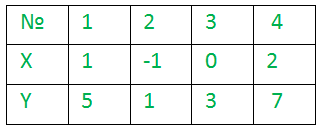
Задача 1. Нарисовать график функции \(2x+3.\)

Решение. Составим табдицу значений функции:

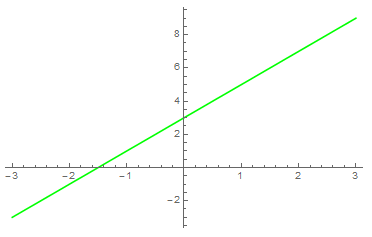
Перенесем на оси координат значения:

Есть много способов дать функцию: по формуле, по графику, по алгоритму, который вычисляет ее, по описанию ее свойств. Иногда функция описывается через ее связь с другими функциями, например, обратная функция. В прикладных дисциплинах функции часто определяются таблицами значений или формулой. Не все типы описания могут быть даны для каждой возможной функции, и необходимо провести четкое различие между самой функцией и несколькими способами ее представления или визуализации.

Функции в алгебре обычно выражаются в терминах алгебраических операций. Функции, изучаемые в анализе, такие как экспоненциальная функция, могут иметь дополнительные свойства, возникающие из непрерывности пространства, но в самом общем случае не могут быть определены одной формулой. Аналитические функции в комплексном анализе могут быть определены довольно конкретно через их разложения рядов. С другой стороны, в лямбда-исчислении функция является примитивным понятием, а не определяется в терминах теории множеств.

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

Предыдущая статья