Чтение графика функций: парабола

Смещение по горизонтали параболы

Если мы прибаляем к функции \(y=x^2\) число 3 \(y=(x+3)^2\), то график смещается по оси \(0X\) на \(-3\) еденицы, если вычитаем число \(2\) \(y=(x-2)^2\), то график сместится \(+2\) относительно \(0X\):

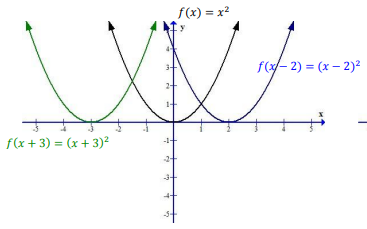
Если мы отнимем от \(y=(x+3)^2\) 3 , то \(y=(x+3)^2-3\), то график начнет смещаться уже по вертикали вниз на \(3\) единицы, а именно по оси \(0Y\):

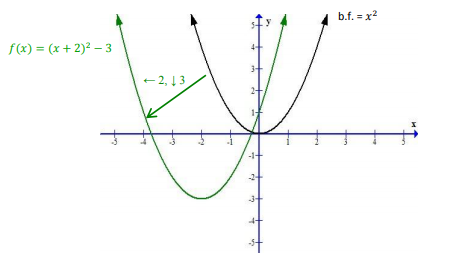
Напомним, графиком квадратичной функции \(y = ax^2 + bx + c \) является парабола, если забыл что такое парабола, то повтори в этой статье https://myalfaschool.ru/articles/parabola. Вершину параболы можно вычислить по формуле: \(x=\frac{ - b}{2a}.\)

Задача

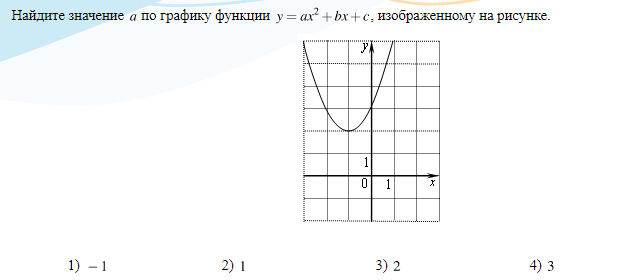
Здесь нам пригодятся знания нахождения формулы вершины параболы \(x=\frac{ - b}{2a}\), она не такая и тяжелая, так что запомните ее. Если мы видим на графике параболу, то сразу представляем уранение вида \(y = ax^2 + bx + c \). По графику выше определяем вершина равна -1:

\(\frac{-b}{2a}=-1\) \(-->\) \(b=2a\)

Как видно из рисунка парабола пересекает \(OY\) в точке 3, поэтому \(с=3\) и \(y = ax^2 + 2ax + 3\), так как \(b=2a\). Находим любую точку проходящую через параболу, возьмем вершину параболы \((-1; 2)\) и подставим в уравнение:

\(2 = (-1)x^2 + 2(-1)x + 3\) \(-->\) \(2=-a+3\) \(-->\) \(a=1\)

Ответ: 2)1.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Павел Юрьевич Осиновой

Репетитор по математике

Стаж (лет)

Образование:

Нижнетагильский государственный социально-педагогический институт (филиал) ФГАОУ ВО

Проведенных занятий:

287

Форма обучения:

Дистанционно (Скайп)

Александр Федорович Каморников

Репетитор по математике

Стаж (лет)

Образование:

Гомельский государственный университет им. Ф. Скорины

Проведенных занятий:

1129

Форма обучения:

Дистанционно (Скайп)

Алина Хамидовна Файрушина

Репетитор по математике

Стаж (лет)

Образование:

Татарский государственный гуманитарно-педагогический университет

Проведенных занятий:

138

Форма обучения:

Дистанционно (Скайп)

Предметы

Специализации