С 10 до 22.00 по МСК ежедневно
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
Решение неравенств с модулем
26 июл 2024
Решение неравенств с модулем
Что такое модуль \(|x-a|\)?
Давайте дадим определение:
И если мы нарисуем картинку, то получим:
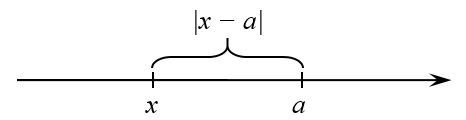
То есть главным моментом будет то, что модуль всегда является числом положительным.
Пример 1. Найдите значение \(\left|6+6x\right|\le \:12\).
Решение :
\(\left|6+6x\right|\le \:12\)
Неравенство с модулем, где модуль меньше или равно какого либо значения \(|a|\le \:b\) является системой , то есть объединение двух интервалов, раскрывается по схеме :
\(\begin{equation*} \begin{cases} a,\;a\le \:b \\a,\; a\ge \:-b \end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 3+2x\le \:7 \\ 3+2x\ge \:-7 \end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 6x\le \:6 \\ 6x\ge \:-18\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x\le \:1 \\ x\ge \:-3\end{cases} \end{equation*}\)
\(-3\le \:x\le \:1\)
Ответ: \(\left[-3,\:1\right]\).
Пример 2. Найдите значение \(\left|5x-9\right|<\:6\).
Решение :
\(\left|5x-9\right|<\:6\)
\(\begin{equation*} \begin{cases} 5x-9<6 \\ 5x-9>-6\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} 5x<15 \\ 5x>3\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x<3\\ x>\frac{3}{5}\end{cases} \end{equation*}\)
\(\begin{equation*} \begin{cases} x<3\\ x>0,6\end{cases} \end{equation*}\)
\(0,6<x<3\)
Ответ: \(\left(0,6;\:3\right)\).
Неравенство с модулем, где модуль больше или равно \(|x|\geq a \) решается по формуле и является совокупностью двух интервалов:
\(\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.\)
Пример 3. Найдите значение \(\left|x-15\right|\ge \:\:3\).
Решение :
\(\left|x-15\right|\ge \:\:3\)
\(\left[ \begin{gathered} x-15\le \:-3\\ x-15\ge \:3 \\ \end{gathered} \right.\)
\(\left[ \begin{gathered} x\le \:12\\ x\ge \:18 \\ \end{gathered} \right.\)
Ответ: \((-\infty \:,\:12]\cup \:[18,\:\infty \:)\).
Пример 4. Найдите значение \(4\left|x+10\right|\ge \:16\).
Решение :
\(4\left|x+10\right|\ge \:16\)
\(\left[ \begin{gathered} x+10\le \:-4\\ x+10\ge \:4\\ \end{gathered} \right.\)
\(\left[ \begin{gathered} x\le \:-14\\ x\ge \:-6\\ \end{gathered} \right.\)
Ответ: \(\:(-\infty \:,\:-14]\cup \:[-6,\:\infty \:)\).
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Репетитор для подготовки к ОГЭ по физике -
![rhombus]()
Подготовка к олимпиадам по физике -
![rhombus]()
Репетитор по грамматике русского языка -
![rhombus]()
Подготовка к олимпиадам по английскому языку -
![rhombus]()
Репетитор по грамматике английского языка -
![rhombus]()
Репетитор для подготовки к ВПР по английскому языку -
![rhombus]()
Репетитор для подготовки к ВПР по обществознанию -
![rhombus]()
Репетитор по географии для подготовки к ЕГЭ -
![rhombus]()
Репетитор по географии для подготовки к ОГЭ -
![rhombus]()
Scratch
Похожие статьи
Чтение графика функций: парабола
26 май 2024
Объем сферы
26 май 2024
Площадь поверхности конуса
26 май 2024
Как перевести квадратные метры в квадратные километры
26 июл 2024
ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
26 фев 2024
Осенняя фотосессия: идеи для креативных снимков
26 июн 2024
Я внучка (внук): взаимоотношения с бабушками и дедушками
26 июл 2024
Почему дети симулируют болезнь
26 янв 2024