percent
img
telegram
О платформе Новое Премиум математика Репетиторы Тарифы
Записаться на урок

Дарим первый урок с репетитором бесплатно

Оставьте заявку и получите первый урок в подарок

bg bg gift

ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 3)

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы Абитурентам Математика Подготовка к ЕГЭ Русский язык ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ Полезное Досуг Физика
#Математика #Подготовка к ЕГЭ #ЕГЭ по математике

Обновлено: 16 дек 2024

ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 3)

 
Условие:
 
Найдите точку максимума функции:
 
у = х3 – 3·х2 + 2
 
Решение
 
Найдем производную заданной функции:
 
у' = 3х2 – 6х = 3х(х – 2)
 
Найдем нули производной:
 
3х(х – 2) = 0
 
х1 = 0
х2 = 2
 
Определим знаки производной функции и изобразим на рисунке (Рис.1) поведение функции:
 
 
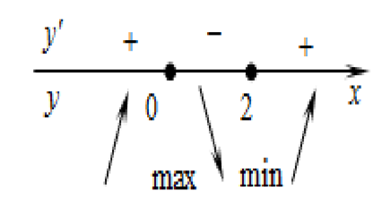
Рис.1 
 
Искомая точка максимума: х = 0 
 
Ответ: 0.
 
 
Предыдущая статья img Следующая статья img

Дарим в подарок бесплатный вводный урок!

line gift
Репетиторы arrow
Специализация arrow

Похожие статьи

img

Решение уравнений с одной переменной

Обновлено: 28 фев 2025

 img

Периметр трапеции

Обновлено: 27 ноя 2024

 img

Параллелограмм

Обновлено: 22 апр 2024

 img

Смещение графиков функций

Обновлено: 25 апр 2024

 img

Формулы параболы

Обновлено: 25 апр 2024

 img

Обратные тригонометрические функции

Обновлено: 17 июн 2024

 img

Как вычислить 50 процентов от числа?

Обновлено: 02 ноя 2024

 img

Задачи на движение по прямой (вариант 1)

Обновлено: 03 апр 2024