Скалярное произведение векторов
Предметы
Специализации
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к ОГЭ по физике
- Английский язык для начинающих
- Репетитор по грамматике английского языка
- ВПР по математике
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по биологии для подготовки к ЕГЭ
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по географии для подготовки к ОГЭ
- Репетитор по информатике для подготовки к ОГЭ
Векторы - это величины, которые описываются как величиной, так и направлением. И для поиска скалярного произведения нужно найти косинус угла между векторами.
Как найти скалярное произведение векторов?
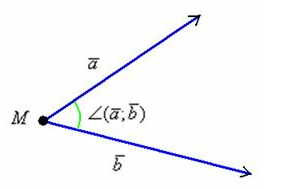
Скалярное произведение \( \overline{a }\) и \( \overline{b }\) определяется как
\( \overline{a }· \overline{b }\) \(= |a| |b|· ∠ (\overline{a }\overline{b })\)
где \(| a |-\) модуль, или величина \( a\),
\(| b |-\) модуль \(b\),
\(∠ (\overline{a }\overline{b })\) - угол между векторами \(a\) и \(b\):
\( \overline{a }· \overline{b }\) \(= |a| |b|· ∠ (\overline{a }\overline{b })\)
где \(| a |-\) модуль, или величина \( a\),
\(| b |-\) модуль \(b\),
\(∠ (\overline{a }\overline{b })\) - угол между векторами \(a\) и \(b\):
Если два вектора сонаправлены, то \( ∠cos (\overline{a }\overline{b })= ∠cos \;0=1\) скалярное произведение равно \( \overline{a }· \overline{b }\)\(=\)\( \overline{|a| }· \overline{|b| }\).
Пример 1. Рассмотрим два вектора \( \overline{a }\) и \( \overline{b }\) модуль \( \overline{a }\) равен \(4\), а \( \overline{b }\) равен \(5\), а угол между ними равен \(60◦\). Найдите скалярное произведение \( \overline{a }· \overline{b }\).
Решение: \( 4 × 5 × cos 60◦ = 4 × 5 ×\frac{1}{2}= 10 \).
Ответ: \(10\).
- Если угол между \( \overline{a }\) и \( \overline{b }\) меньше \(90◦\) , то есть расположен на промежутке \(0<∠ (\overline{a }\overline{b })<\frac{\pi}{2}\), то результат скалярного произведения будет больше \(0\) , то есть положительным.
- Если угол между \( \overline{a }\) и \( \overline{b }\) больше \(90◦\) , то есть расположен на промежутке \(\frac{\pi}{2}<∠ (\overline{a }\overline{b })<\pi\) , то результат скалярного произведения будет меньше \(0\) , то есть отрицательным.
- Если угол между \( \overline{a }\) и \( \overline{b }\) равен \(90◦\), то результат скалярного произведения будет равен \(0\), так как \(cos\frac{\pi}{2}=0\).
Пример 2. Даны два вектора \( \overline{с }= -2\overline{a }+\overline{b }\) и \(\overline{d }=\overline{a }-\overline{b }\) , \(\overline{|a| }=4\sqrt{3}\) и \(\overline{|b| }=8\). Найти их скалярное произведение, если угол между ними равен \(45◦\).
Решение: Найдем произведение: \((-2\overline{a }+\overline{b })(\overline{a }-\overline{b })=-2\overline{a }*\overline{a }+\overline{b }*\overline{a } +2\overline{a }*\overline{b }-\overline{b }*\overline{b }=-2\overline{a }^2+\overline{a }*\overline{b }+2\overline{a }*\overline{b }-\overline{b }^2=-2\overline{a }^2+3\overline{a }*\overline{b }-\overline{b }^2\)
Подставим угол \(45◦\) и значения: \(-2\overline{a }^2+3\overline{a }*\overline{b }* cos∠(\overline{a }\overline{b })-\overline{b }^2=-2*(4\sqrt{3})^2+3*4\sqrt{3}*8*cos∠45-8^2=-64+96\sqrt{2}*\frac{\sqrt{2}}{2}-64=32\).
Ответ: \(32\).
Часто задаваемые вопросы:
✅ Как интерпретировать скалярное произведение векторов?
↪ Скалярное произведение позволяет определить, насколько два вектора сонаправлены друг с другом. Если скалярное произведение положительное, векторы направлены близко друг к другу. Если отрицательное, они направлены в противоположные стороны.
✅ Каким свойством обладает скалярное произведение векторов?
↪ Скалярное произведение коммутативно, то есть a·b = b·a.
✅ Для чего используется скалярное произведение в реальных задачах?
↪ Скалярное произведение используется в физике, геометрии, инженерии и других областях для анализа направлений векторов, вычисления работ и энергий, определения проекций и углов между векторами.
Наши преподаватели
Репетитор по математике
Стаж (лет)
5
Образование:
Мозырский государственный педагогический университет им. И.П.Шамякина
Проведенных занятий:
550
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
27
Образование:
Стерлитамакский государственный педагогический институт
Проведенных занятий:
437
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
19
Образование:
КГАУ
Проведенных занятий:
4095
Форма обучения:
Дистанционно (Скайп)
Похожие статьи