Пропорция в математике

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Что такое пропорция: определение
Свойство пропорции
Часто задаваемые вопросы:

Обновлено: 13 фев 2024

Пропорция в математике

Что такое пропорция: определение

Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный - значит находящийся в определенном отношении к какой-либо величине. Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac{4}{2}=\frac{8}{4}\).

Свойство пропорции

Произведение крайних членов пропорции равно произведению средних.

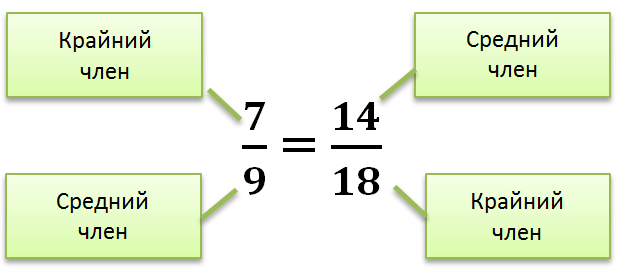
Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.

Если \(\frac{A}{B} = \frac{C}{D}\), то

\(AB=CD\)
\(AD=BC\)

Правило пропорции в том, что пропорция состоит из двух равных отношений. Однако если \(\frac{A}{B}\) не равно \(\frac{C}{D}\), то \(A, B, C, D \) не называются пропорцией.

Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.

\(A, B , C\) находятся в постоянной пропорции, если \(\frac{A}{B} =\frac{C}{D}\)

Если \(A, B ,C \) находятся в постоянном отношении, то \(B\) называется средней в пропорции.

В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.

Задача 1. За \(5\) дней и \(12\) человек построили забор. Сколько дней это займет у \(6\) людей?

Решение.

\(12\) человек → \(5\) дней
\(6\) человек → \(x\) дней
\(\frac{12}{6} = \frac{x}{5}\)
умножаем крест на крест члены пропорции и сокращаем на \(6\):

\(12*5=6x\)

\(60=6x\)

\(x=10\)

Ответ: \(6\) людей будут работать \(10\) дней, чтобы закончить работу.

Задача 2. Найдите значение \(x\), если \(\frac{2}{5}=\frac{x}{15}\)

Решение:

\(2*15=5x\)
\(30 =5x\)
Делим на 5 обе части равенства: \(\frac{30}{5}=x\), откуда находим

Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?

Решение:\(\)

\((10+x)(18+x)=(22+x)(38+x)\)
\(380+48x+2x=396+40x+2x\)
\(8x=16\)
\(x=2\)

Задача 4. Найти четвертый член пропорции \(6,10\) и \(12\)

Решение:

\(\frac{6}{10}=\frac{12}{x}\)

6×х = 120

x = 120/6

x = 20

Часто задаваемые вопросы:

✅ Что такое пропорция в математике?

↪ Пропорция - это равенство двух отношений, в которых те же самые величины сравниваются между собой.

✅ Как записать пропорцию в математике?

↪ Пропорция записывается в виде a:b = c:d или в виде a/b = c/d, где a, b, c и d - числа, называемые пропорциональными величинами.

✅ Как решать задачи на пропорциональное распределение?

↪ Чтобы решить задачу на пропорциональное распределение, необходимо использовать правило трех пропорций. Это правило устанавливает связь между тремя пропорциональными величинами и позволяет найти неизвестную величину.

Предыдущая статья