Система линейных уравнений

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Рассмотрим два линейных уравнения: \(2x-5y-3=0\) и \(2x+5y-5=0\) и найдем их общее решение. Складываем оба уравнения:

Пример системы линейных уравнений

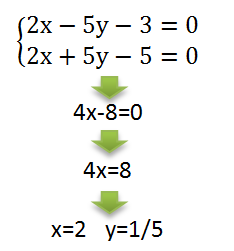
в результате мы получаем общее решение для двух уравнений \(х=2\) и \(y=\frac{1}{5}\), то есть получили пару чисел \((2;\frac{1}{5})\). В круглых скобках мы записываем по порядку сначала \(x\), затем \(y\) \(-(x;y)\).

Дадим определение понятию системы линейных уравнений:

Система линейных уравнений

Записываем систему уравнений с помощью фигурных скобок:

\(\begin{equation*} \begin{cases} a_0x+b_0y=c_0 \\ a_1x+b_1y=c_1 \end{cases} \end{equation*}\)

где \(a_0,b_0,c_0,a_1,b_1,c_1-\) какие-то заданные числа и система имеет решение.

Давайте введем еще одно определение:

Варианты возможных решений системы уравнений с двумя переменными:

система имеет одно единственное решение;
система не имеет решения;
система имеет бесконечно много решений.
система имеет несколько решений

Решить систему уравнений - значит найти значения переменных либо доказать что решения нет.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Особенности решения текстовых задач

Обновлено: 23 мар 2025

Основное свойство дробей

Обновлено: 04 сен 2024

Функция

Обновлено: 18 июл 2024

Производная

Обновлено: 26 авг 2024

Площадь треугольника

Обновлено: 01 сен 2024

Как найти делимое?

Обновлено: 01 мар 2025

ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 1)

Обновлено: 04 окт 2024

ЕГЭ по математике, базовый уровень. Задачи на совместную работу (вариант 4)

Обновлено: 03 дек 2024