Многочлены

Давайте вспомним, что такое многочлен из школьного определения:

Приведем пример многочленов \(a^2+2b+c^3; t^4+3ab^3\). То есть многочлен состоит из суммы одночленов:

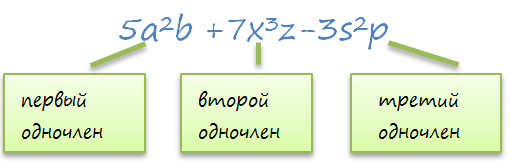
Однако у нас в многочлене присутствует минус, хотя мы его тоже называем многочленом.

Все просто решается, если мы это минус отнесем к числовому коэффициенту, то у нас получится алгебраическая сумма:

Часто в задачах нас просят найти степень многочлена - это наибольшая степень из всех одночленов. Из примера выше степень многочлена равна 3.

Подобные члены в многочлене:

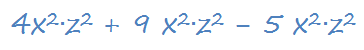
Привести все подобные одночлены в многочлене значит сложить или вычесть все числовые коэффициенты

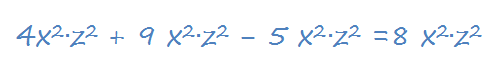
Свободным членом в многочлене называется число без буквенной части:

Свойства многочленов:

Одночлены можно менять местами, не забывая ставить соответствующие знаки числовых коэффициентов, которые относятся к ним.
Прибавление нуля не изменит его значения
Если мы приведем подобные члены, значение выражения не изменится
Если мы прибавим и отнимем один и тот же одночлен или число, значение выражения не изменится
Одночлен в многочлене можно разложить на два подобных одночлена, чтобы при сумме они давали первоначальное значение.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Аурика Витальевна Чуева

Репетитор по математике

Стаж (лет)

Образование:

ГОУ

Проведенных занятий:

115

Форма обучения:

Дистанционно (Скайп)

Виктор Дмитриевич Ильин

Репетитор по математике

Стаж (лет)

Образование:

ГОУ ВО Луганский государственный университет имени Владимира Даля, Кафедра теории и практики перевода германских и романских языков факультета филологии и массовых коммуникаций

Проведенных занятий:

171

Форма обучения:

Дистанционно (Скайп)

Наталья Евгеньевна Блехер

Репетитор по математике

Стаж (лет)

Образование:

Казанский инженерно- строительный институт

Проведенных занятий:

140

Форма обучения:

Дистанционно (Скайп)

Предметы

Специализации