Сравнение дробей

 
Что больше \(\frac{4}{7}\) или  \(\frac{5}{9}\), \(\frac{3}{13}\) или \(\frac{11}{45}\)? Для дробных чисел, таких как \(\frac{1}{4}\), \(\frac{1}{3}\) и \(\frac{1}{2}\), которые вы можете легко визуализировать, ответить на такие вопросы относительно легко. Но с такими дробями, как \(\frac{4}{7}\), \(\frac{5}{9}\), \(\frac{3}{13}\) и \(\frac{11}{45}\), ответ не совсем очевиден. Так как вы это делаете? Каков наилучший способ сравнить дроби, чтобы вы могли выстроить их в порядке возрастания или убывания? Продолжайте читать, потому что это именно то, что мы рассмотрим сегодня.
 
Упорядочивание дробей происходит в порядке возрастания или убывания. Дроби, которые должны быть упорядочены, могут быть с одинаковыми или неодинаковыми  знаменателями.
 
Если мы должны сравнить две дроби с разными знаменателями, мы пишем их эквивалентные дроби. Для этого нам понадобиться вычислить НОК у знаменателей этих дробей. Затем мы сравниваем их числители и получаем нужное нам сравнение.
 
Задача 1. Сравните две дроби \(\frac{9}{11}\) и \(\frac{5}{6}\)
Решение.
 
Сравнение дробей
 
 
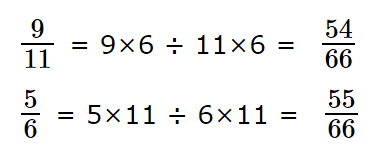
  1. Найдем у этих дробей \(\frac{9}{11}\) и \(\frac{5}{6}\) общий знаменатель, с помощью НОK чисел. У дробей \(\frac{9}{11}\) и  \(\frac{5}{6}\) это  \(66\).
  2. Затем используем знак "<",  "=" или ">" для сравнения числителей приведенных дробей.
  3. Поскольку \(\frac{54}{66}\) и \(\frac{55}{66}\) имеют общий знаменатель, мы можем сравнить их, используя их числители.Так как \(54<55\), то, очевидно, вторая дробь больше:
Дроби
 
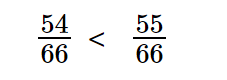
      Записываем в первоначальном виде :
Сравнение
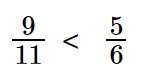
Вывод:
  1. Мы должны переписать дроби так, чтобы они имели общий знаменатель.
  2. Нам необходимо найти наименьший общий знаменатель.
  3. Сравниваем числители.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анна Михайловна Глущенко
Репетитор по математике
Стаж (лет)
23
Образование:
Восточная экономико-юридическая гуманитарная академия
Проведенных занятий:
377
Форма обучения:
Дистанционно (Скайп)
Никита Сергеевич Анохин
Репетитор по математике
Стаж (лет)
3
Образование:
Керченский государственный морской технологический университет
Проведенных занятий:
373
Форма обучения:
Дистанционно (Скайп)
Юлиана Евгеньевна Соловьёва
Репетитор по математике
Стаж (лет)
20
Образование:
Воронежский государственный педагогический университет
Проведенных занятий:
171
Форма обучения:
Дистанционно (Скайп)
Предметы
Специализации
Похожие статьи