Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Планиметрическая задача
Условие:
Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T. Точка O лежит внутри трапеции ABCD.а) Докажите, что угол BOC вдвое больше угла BCТ.б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.
Решение
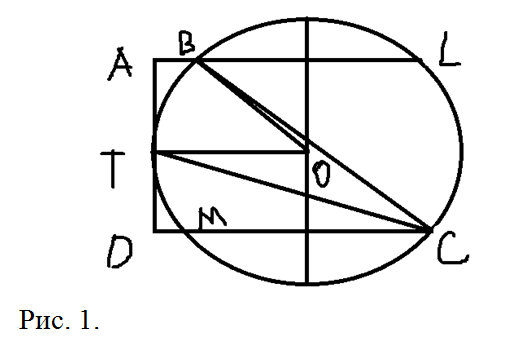
а) Выполним чертеж, согласно условию задачи (Рис.1). Из чертежа видно, что угол BCТ вписан в окружность, а угол BOC является соответствующим ему центральным углом. Согласно свойствам вписанного и центрального углов, ∠BOC = 2∠BCТ. Что и требовалось доказать.
б) По условию задачи, окружность и сторона AD касаются в точке Т. Следовательно, из условия задачи, что АВСD – прямоугольная трапеция, тогда прямые OT и AD перпендикулярны. Обозначим точку, в которой окружность вторично пересекает прямую AB как L, а сторону CD — точкой M. Тогда получим, что диаметр окружности, перпендикулярный стороне AB, делит каждую из хорд BL и CM пополам (на Рис.1. диаметр проведен вертикальной линией). Обозначим OT = r, тогда:
AL = 2r − AB = 2r − 4, DM = 2r − CD = 2r − 9.
По теореме Пифагора, получим:
\(TB^2=AT^2+AB^2\)
По теореме о касательной и секущей, получим:
\(AT^2=AB*AL=4(2r-4)\)
Отсюда следует, что:
\(TB^2=4(2r-4)+4^2=8r\)
Рассуждая подобным образом, получим:
\(TC^2=18r\)
Далее из теоремы синусов получим, что:
BC = 2r · sin ∠BTC.
Обозначим через «h» искомое расстояние от точки T до прямой BC. Далее, выразим площадь треугольника BTC двумя способами:
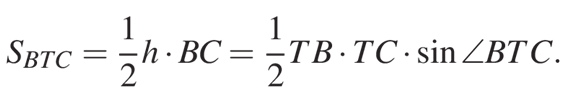
Отсюда получаем, что:
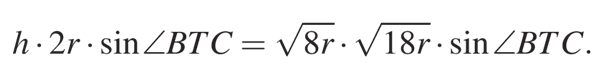
После преобразований, получаем:
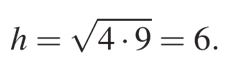
Ответ: 6
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор для подготовки к ОГЭ по математике
Репетитор для подготовки к ОГЭ по математике -
 Репетитор по алгебре
Репетитор по алгебре -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Подготовка к олимпиадам по физике
Подготовка к олимпиадам по физике -
 Подготовка к ОГЭ по русскому 9 класс
Подготовка к ОГЭ по русскому 9 класс -
 Подготовка к сочинению по русскому языку
Подготовка к сочинению по русскому языку -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Репетитор по истории ОГЭ
Репетитор по истории ОГЭ -
 Репетитор по биологии ЕГЭ 2024
Репетитор по биологии ЕГЭ 2024 -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

