Топ-5 тем по геометрии, в которых чаще всего совершают ошибки

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

1. Неравенство треугольника. Каждая сторона треугольника меньше суммы двух других сторон
2. Теорема: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
3. Отношение площадей и объемов подобных фигур. Отношение площадей двух подобных фигур равно квадрату коэффициента подобия, а отношение объемов двух подобных фигур равно кубу коэффициента подобия
4. Пропорциональные отрезки в прямоугольном треугольнике
5. Теорема: если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды

Топ-5 тем по геометрии, в которых чаще всего совершают ошибки

Преподаватель математики Ольга Геннадьевна рассматривает 5 самых проблемных тем по геометрии.

1. Неравенство треугольника. Каждая сторона треугольника меньше суммы двух других сторон

Данная теорема используется при построениях, а чаще всего построения делаются интуитивно. В результате, если требуется распределить стороны и углы, то делается это наугад. А ведь есть такая прекрасная теорема. Здесь же хотела напомнить еще одно утверждение:

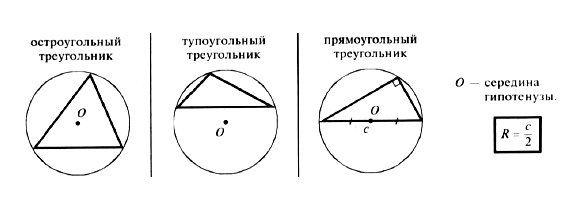
центр описанной около треугольника окружности лежит: на середине гипотенузы, если треугольник прямоугольный, внутри треугольника, если треугольник остроугольный и вне треугольника, если треугольник тупоугольный.

2. Теорема: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы

Т.е. если

$S$ и

$S1$ - площади треугольников

$ABC$ и

$A1B1C1$ , у которых

$<A=<A1$ то

${{s}\over {s_1}} = {AB⋅AC\over A_1 B_1⋅A_1 C_1 }$

Но чаще всего эта теорема встретится в таком варианте: $B$ ∆ $ABC$ стороны $AB=5$ , $AC=10$ , $S∆=100$ . Через т.M принадлежащей стороне $AB$ , проходит прямая, параллельная стороне $BC$ , так, что $AM:MB=2:3$ , Найти $S∆$ который отсекается этой прямой от $∆ABC$ .

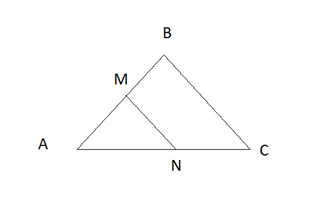
Решение: По Т.Фалеса прямая пересечет сторону

$AC$ в т.

$N$ , в том же отношении. Значит стороны

$AM=5:5*2=2$ ,

$AN=10:5*2=4$ .

Тогда, по данной теореме составим пропорцию:

${{100}\over {s_ΔAMN}} ={5⋅10\over 2⋅4}$

Решив ее, найдем

${s_ΔAMN}={100⋅2⋅4\over 5⋅10}={16}$

3. Отношение площадей и объемов подобных фигур. Отношение площадей двух подобных фигур равно квадрату коэффициента подобия, а отношение объемов двух подобных фигур равно кубу коэффициента подобия

Задание на применение данного свойства есть и в ОГЭ, и в ЕГЭ (профиль и база), но ученики продолжают говорить, что не знают подобного. А ведь применение этого свойства в разы упрощает решение.

Вот пример из пособия по подготовке к ЕГЭ. Площадь треугольника $ABC=8$ . $DE$ -средняя линия. Найдите площадь треугольника $CDE$

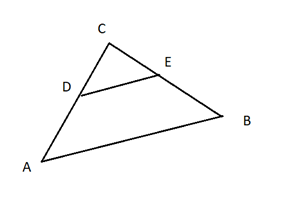
Решение: Так как

$DE$ - средняя линия, значит

${DE\over AB}={1\over2}=k$ , тогда

${s_ΔCDE\over s_Δ ACB}=k^2=(1/2)^2=1/4$ . Подставив в пропорцию

${s_ΔCDE\over s_Δ ACB}={1\over 4}$ , известные данные, получим

${s_ΔCDE\over 8}={1\over 4}$ , откуда

$s_ΔCDE={8\over 4}=2$

4. Пропорциональные отрезки в прямоугольном треугольнике

Данную тему проще запомнить по рисунку:

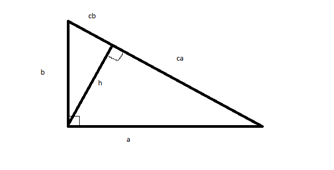
Вот если у вас такая ситуация, то

$h^2=cb⋅ca$

$b^2=c⋅cb$

$a^2=c⋅ca$

$h= {a⋅b\over c}$

Например: В треугольнике $ABC$ , изображенном на рисунке, известно, что $<ABC$ =90⁰, $BD⊥AC$ , $AD=12см$ , $CD=16см$ . Найдите длины сторон BC,AB,BD.

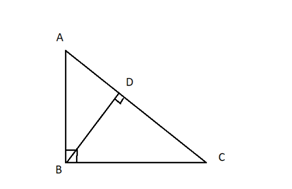
Решение:

$BD$ ^{2 = $AD•DC=12•16=192 , тогда BD= √192=8√3$}

$AB$ ²=

$AC•AD=(12+16)•12=336 , тогда AB= √336=4√21$

$BC$ ²=

$AC•DC=(12+16)•16=448 , тогда BC= √448=8√7$

Используйте эти формулы, и геометрия станет легче.

5. Теорема: если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды

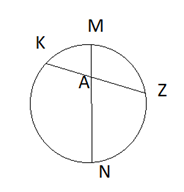
Например: Хорды $MN$ и $KZ$ окружности пересекаются в точке $A$ , причем хорда $MN$ делится точкой $A$ на отрезки, равные 1 см и 15 см. На какие отрезки точка $A$ делит хорду $KZ$ , если длина $KZ$ в 2 раза меньше длины $MN$ ?

Решение: Если т.

$A$ делит

$MN$ на отрезки 1 и 15, то

$MA=1$ ,

$NA=15$ . Так как

$KZ$ в 2 раза меньше

$MN$ , то

$KZ=(1+15):2=8$ , значит

$:KA+AZ=8$ , отсюда

$KA=8-AZ$ , по теореме

$MA•AN=KA•AZ$

$1•16=(8-AZ)•AZ$ . Открыв скобки, получаем

$16=8AZ-AZ$ ², перенесем все вправо, получим квадратное уравнение

$AZ$ ²

$-8AZ+16=0$ ,его

$дискриминант =0, AZ=4, тогда KA=4.$

Итак, перед вами пять самых забываемых тем. Что с ними делать? Выучить, конечно. Но и этого недостаточно. Разобранные примеры нужно применять на практике. Чем чаще вы занимаетесь, тем меньше забываете!

Предыдущая статья