Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



ЕГЭ по математике, профильный уровень. Уравнение смешанного типа
Условие:
а) Решите уравнение
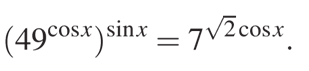
б) Найдите все корни этого уравнения, принадлежащие отрезку 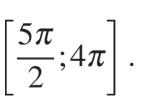
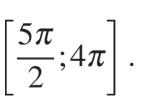
Решение
а) Перед нами уравнение смешанного типа. Мы видим, что имеется степень, поэтому мы можем отнести это уравнение к показательным. При этом в качестве показателей степени мы видим тригонометрические функции, с которыми нам также придется поработать.
Для начала преобразуем исходное уравнение так, чтобы у нас получились одинаковые основания степени, что позволит нам перейти к уравнению без них:
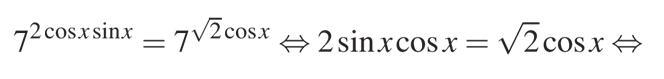
Получившееся тригонометрическое уравнение будем решать через вынос за скобку «cos x». Это позволит нам получить произведение множителя и скобки. После этого преобразования мы решим это уравнение, как систему двух более простых тригонометрических уравнений:
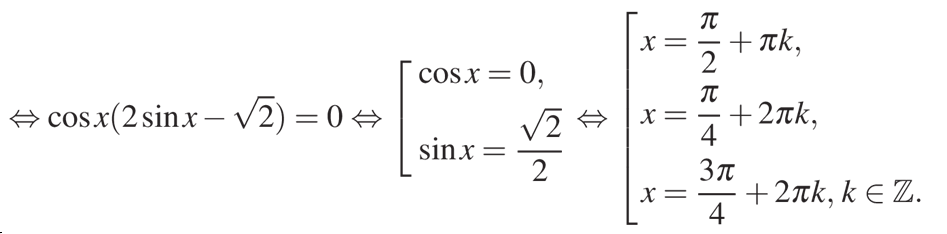
Итак, мы получили три корня.
б) Теперь с помощью единичной окружности или числовой прямой отберём все корни, принадлежащие заданному отрезку:
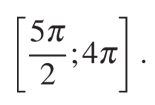
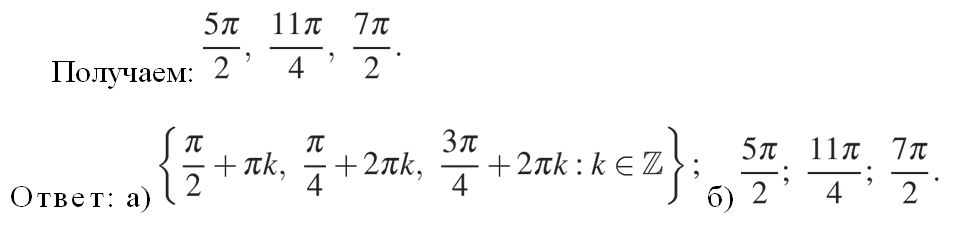
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор для подготовки к ОГЭ по математике
Репетитор для подготовки к ОГЭ по математике -
 Подготовка к олимпиадам по физике
Подготовка к олимпиадам по физике -
 Подготовка к ЕГЭ по английскому онлайн
Подготовка к ЕГЭ по английскому онлайн -
 Подготовка к ЕГЭ по истории
Подготовка к ЕГЭ по истории -
 ВПР по физике
ВПР по физике -
 Репетитор по обществознанию ВПР
Репетитор по обществознанию ВПР -
 Подготовка к ЕГЭ по биологии онлайн
Подготовка к ЕГЭ по биологии онлайн -
 Репетитор для подготовки к ЕГЭ по географии
Репетитор для подготовки к ЕГЭ по географии -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Репетитор Scratch
Репетитор Scratch


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

