Площадь параллелограмма

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Площадь параллелограмма: основные формулы
Площадь параллелограмма

Немного из истории

Необходимость нахождения площади параллелограммов и их частных случаев – прямоугольников, возникла очень давно. С древних времен человеку необходимо было находить площади земельных участков для сельскохозяйственных нужд и градостроительства.

Площадь параллелограмма: основные формулы

Существует несколько формул нахождения площади параллелограмма. Каждая из них подходит для решения соответствующего круга задач.

Рассмотрим основные формулы.

Площадь параллелограмма

Площадь параллелограмма через одну из его сторон и высоту, проведенную к этой стороне:

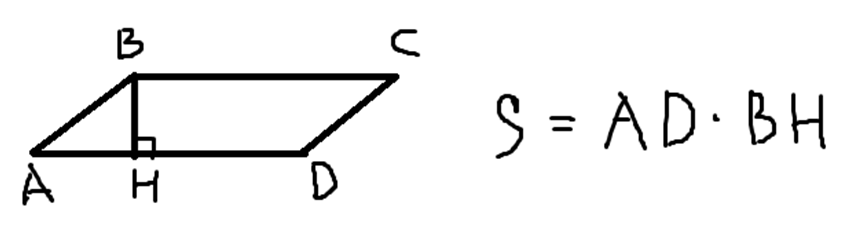
Площадь параллелограмма через две его стороны и синус угла между ними:

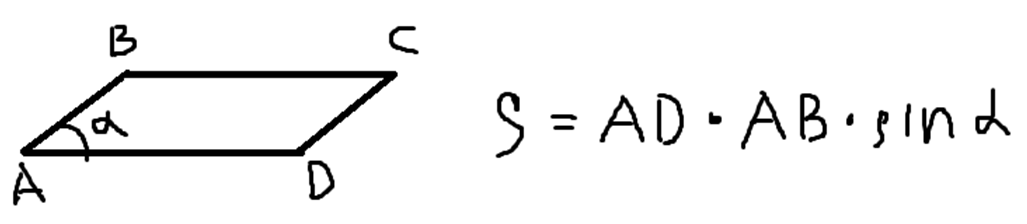
Площадь параллелограмма через его диагонали и угол между ними:

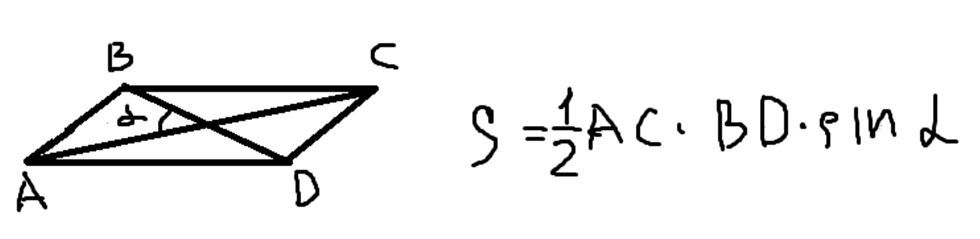
Давайте разберем задачу, иллюстрирующую применение одной из этих формул:

Задача

Даны параллелограмм АВСD и прямоугольник EFKM, которые имеют одинаковую длину соответствующих сторон (см. рисунок ниже). Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

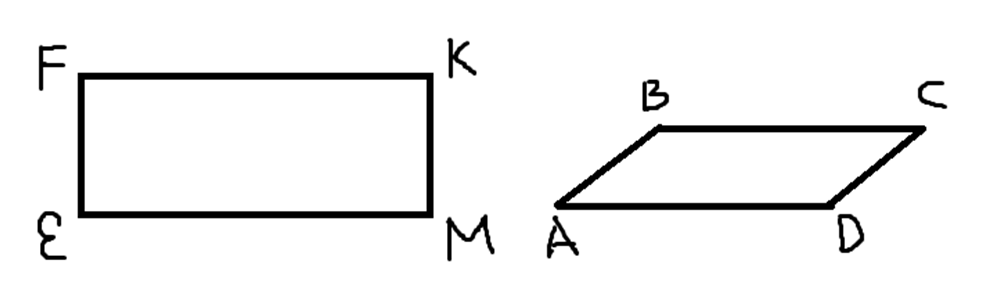
Решение

На первый взгляд, это очень сложная задача, так как мы не знаем ни одного конкретного параметра ни одной из этих геометрических фигур. Давайте попробуем разобраться.

По условию задачи, стороны FE = АВ, КМ = СD, ЕМ = АD, FК = ВС.

Площадь параллелограмма в данном случае удобно найти через две стороны и синус угла между ними (2-я формула). Площадь прямоугольника в классическом прочтении равна произведению длины на ширину. Но так как прямоугольник – это частный случай параллелограмма, то его площадь также можно представить через две стороны и синус угла между ними. Только в этом случае угол будет равен 90 градусов, а синус 90 градусов равен «1». Поэтому значительно проще при нахождении площади прямоугольников обходится без синусов.

Так как по условию задачи соответствующие стороны прямоугольника и параллелограмма равны, мы можем их обозначить одной буквой:

FE = АВ = Х

ЕМ = АD = У

Острый угол, например, ВАD обозначим одной буквой А.

Тогда площадь параллелограмма равна:

Sпар = ХУsinA

а площадь прямоугольника равна:

Sпрям = ХУ

Также по условию площадь прямоугольника вдвое больше площади параллелограмма:

Sпрям = 2 Sпар

Следовательно, мы можем записать следующее уравнение:

ХУ = 2 ХУ sinA

Сокращаем обе части этого уравнения на «Х У», получаем:

1 = 2 sinA

Откуда:

sinA = 0,5

По таблице синусов находим, что если sinA = 0,5, то угол А = 30 градусов

Ответ: 30

Как видите, иногда, зная только один сравнительный параметр, связывающий две геометрические фигуры, мы можем вычислить некоторые параметры одной из фигур, опираясь только на знание формул для нахождения площади этих фигур.