ЕГЭ по математике, профильный уровень. Окружности и четырехугольники

Математика Подготовка к ЕГЭ ЕГЭ по математике

Предлагаем разобрать задачу, приведенную ниже. Это задание №16 из ЕГЭ прошлых лет.

Условие:

Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.

а) Докажите, что трапеция ABCD равнобедренная.

б) Известно, что радиус этих окружностей равен 3, а меньшее основание BC исходной трапеции равно 8. Найдите радиус окружности, касающейся боковой стороны AB, основания AN трапеции ABMN и вписанной в неё окружности.

Решение

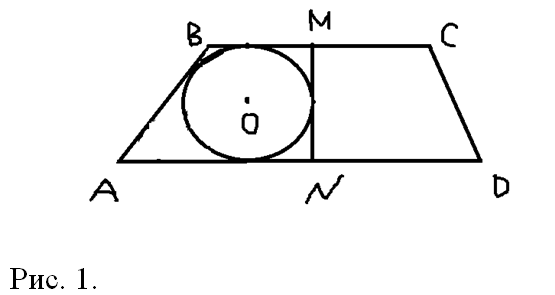
а) Выполним чертеж, согласно условию задачи (Рис.1). Из условия, что в трапецию вписаны две окружности, следует, что:

ВМ+AN=AB+MN и MC+ND=CD+MN

Поскольку из условия задачи: BM=MC и AN=ND получаем, что AB=CD

Значит, трапеция ABCD – равнобедренная. Что и требовалось доказать.

б) Дополним чертеж, согласно условию задачи (Рис. 2).

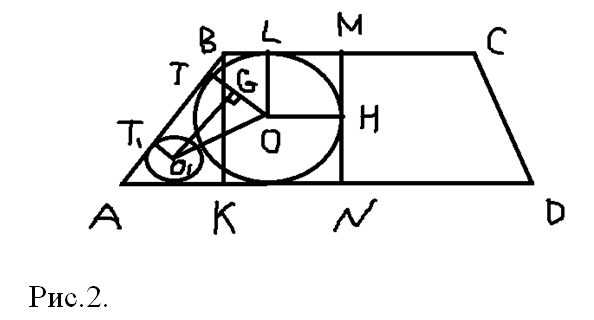
Очевидно, при этих условиях отрезок MN является высотой трапеции и имеет длину 6.

Обозначим AN = t, тогда из условия, что в трапецию вписаны две окружности, рассматривая трапецию BMNA, получим:

AB+6=t+4,

откуда AB= t-2

Сделаем дополнительные построения, опуская высоту BK, получим:

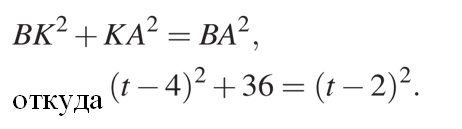
Решая это уравнение, получаем t=12 и AB=10

Обозначим точкой O — центр окружности, вписанной в BMNA,

Обозначим точкой O1 — центр второй окружности

Обозначим их проекции на сторону AB точками T и T1 соответственно,

радиус второй окружности обозначим r.

Тогда TOO1T1 — трапеция, в которой:

TO=3, T1O1=r, OO1=3+r

Опустим из точки O перпендикуляры OL и OH на BM и MN соответственно.

Тогда OLMH — квадрат со стороной 3, поэтому:

BT=BL=4-3=1, а AT=9

Из подобия треугольников ATO и AT1O1 находим, что:

AT1=3r и TT1=9-3r

Теперь опустим перпендикуляр O1G на OT.

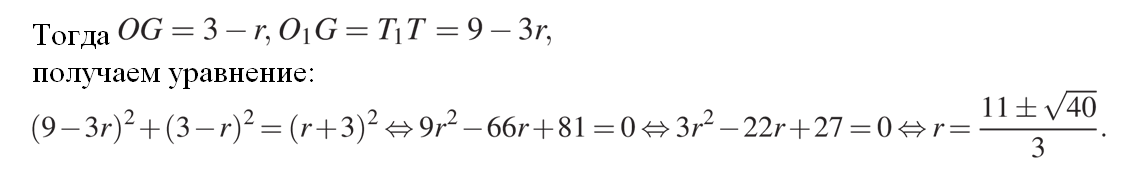
Из двух корней этого уравнения подходит только меньший, поскольку r<3

Предыдущая статья

Следующая статья

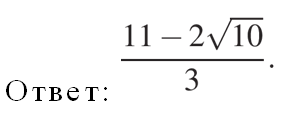
Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Что такое дробные числа?

Обновлено: 23 июн 2024

Сложение смешанных дробей

Обновлено: 18 мар 2025

Параллелограмм

Обновлено: 19 янв 2025

Примеры решения неравенств

Обновлено: 27 июн 2024

Cреднее арифметическое: примеры решения

Обновлено: 03 фев 2025

Как перевести квадратные дециметры в квадратные метры

Обновлено: 26 мар 2025

Задача по планиметрии

Обновлено: 23 июл 2024

Решаем ОГЭ по математике. Задание №5. 2

Обновлено: 21 мар 2025